Viernes 25 de noviembre
*Resolverán en parejas el REPASO sobre Teorema de Pitágoras (aunque el día del examen deberán engraparlo junto con el examen de manera individual).
Lunes 28 de noviembre
*Contestarán el examen rápido sobre Índices.
*Si les queda tiempo y no han terminado el REPASO de Teorema de Pitágoras, pueden terminarlo en lo que resta de la clase.
*Recuerden pegar y repasar muy bien los ejemplos del Blog y los ejercicios.
Martes 29 de noviembre
*Resolverán el examen de Teorema de Pitágoras. Tienen toda la hora para contestarlo. No se apresuren.
Miércoles 30 de noviembre
* Llevarán los materiales para trabajar en en su proyecto. Yo les daré el previamente las copias con las especificaciones del mismo.
RECUERDEN QUE:
*En todo momento usar la calculadora para sus actividades. Sólo no está permito el prestarse ningún material durante las actividades o exámenes rápidos.
*SÓLO ALUMNOS ANDES: Hay asesorías para matemáticas 3, este viernes 25 de 5:40 en delante, por si alguno tiene alguno duda sobre el tema de Teorema de Pitágoras, yo estaré en el cuarto piso en el salón de 2° A o 2° B.
miércoles, 23 de noviembre de 2011
lunes, 14 de noviembre de 2011
PROYECTO BIMESTRAL 2
Selecciona junto con tu equipo alguna de las siguientes opciones:
Opción 01: Deberán diseñar y amar tres cajas según las siguientes indicaciones:
Las cajas serán elaboradas con cartón o cartulina pintadas de distinto color.
Indicarán la medida de ancho, longitud, altura de la base y volumen para cada una.
Decidirán para qué podrían utilizarse según sus dimensiones, por ejemplo, para lápices en el escritorio, pañuelos desechables, cuadernos, etc.
Al finalizarlas, realizarán una exposición.
Opción 02: Explicarán un método de solución que sirva para resolver ecuaciones cuadráticas.
Para ello, realizarán una tabla que les ayude a resolver cuatro ecuaciones, las cuales se les mostrarán más adelante.
Opción 03: Diseñarán un póster que contenga figuras y objetos semejantes.
Podrán utilizar materiales de su elección, como cartulina, cartoncillo, papel cascarón o ilustración, lápices de colores, plumones y un juego de geometría para realizar sus dibujos o trazos.
Opción 04: Elaborarán un informe en el que describirán el procedimiento para calcular cuánto mide un objeto o estructura de gran altura.
Para ello deberán elegir un edificio o monumento cuya altura no puedan calcular directamente. Puede ser, por ejemplo, el lugar donde viven (casa, edificio), un árbol muy alto que esté en su localidad, etc.
Deberán presentar al profesor, y a todo el grupo, una fotografía o dibujo del objeto o estructura que eligieron medir y dos estrategias para calcular su altura. Dichas estrategias tendrán que justificarse geométricamente.
Opción 05: Realizarán una investigación del Índice Nacional de Precios al Consumidor (INPC) o del Índice de Desarrollo Social en México, los cuales son muy utilizados para medir la economía y el desarrollo del país.
Entregarán al profesor un reporte de su investigación y explicarán sus resultados ante el grupo.
Opción 06: Diseñarán una manera de simular el juego de la ruleta. Para comenzar consideren una ruleta de cinco colores.
Discutan cómo pueden realizar la simulación del juego de la ruleta, sin tenerla físicamente.
Realizarán un total de 200 simulaciones.
Elaborarán una presentación en la que expliquen cómo llevaron a cabo la simulación y cuáles fueron los resultados que obtuvieron.
Opción 01: Deberán diseñar y amar tres cajas según las siguientes indicaciones:
Las cajas serán elaboradas con cartón o cartulina pintadas de distinto color.
Indicarán la medida de ancho, longitud, altura de la base y volumen para cada una.
Decidirán para qué podrían utilizarse según sus dimensiones, por ejemplo, para lápices en el escritorio, pañuelos desechables, cuadernos, etc.
Al finalizarlas, realizarán una exposición.
Opción 02: Explicarán un método de solución que sirva para resolver ecuaciones cuadráticas.
Para ello, realizarán una tabla que les ayude a resolver cuatro ecuaciones, las cuales se les mostrarán más adelante.
Opción 03: Diseñarán un póster que contenga figuras y objetos semejantes.
Podrán utilizar materiales de su elección, como cartulina, cartoncillo, papel cascarón o ilustración, lápices de colores, plumones y un juego de geometría para realizar sus dibujos o trazos.
Opción 04: Elaborarán un informe en el que describirán el procedimiento para calcular cuánto mide un objeto o estructura de gran altura.
Para ello deberán elegir un edificio o monumento cuya altura no puedan calcular directamente. Puede ser, por ejemplo, el lugar donde viven (casa, edificio), un árbol muy alto que esté en su localidad, etc.
Deberán presentar al profesor, y a todo el grupo, una fotografía o dibujo del objeto o estructura que eligieron medir y dos estrategias para calcular su altura. Dichas estrategias tendrán que justificarse geométricamente.
Opción 05: Realizarán una investigación del Índice Nacional de Precios al Consumidor (INPC) o del Índice de Desarrollo Social en México, los cuales son muy utilizados para medir la economía y el desarrollo del país.
Entregarán al profesor un reporte de su investigación y explicarán sus resultados ante el grupo.
Opción 06: Diseñarán una manera de simular el juego de la ruleta. Para comenzar consideren una ruleta de cinco colores.
Discutan cómo pueden realizar la simulación del juego de la ruleta, sin tenerla físicamente.
Realizarán un total de 200 simulaciones.
Elaborarán una presentación en la que expliquen cómo llevaron a cabo la simulación y cuáles fueron los resultados que obtuvieron.
12 Índices
Objetivo: En esta secuencia aprenderás a interpretar y utilizar índices para explicar el comportamiento de diversas situaciones.
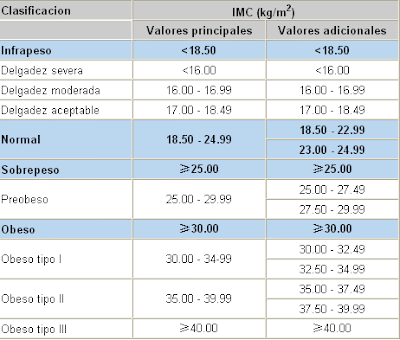
EJEMPLO 1: EL ÍNDICE DE MASA CORPORAL
Índice de Masa Corporal (IMC) - El IMC se calcula dividiendo el peso por el cuadrado de la altura. El número da una idea de la proporción del cuerpo. En general, el número es pequeño para las personas delgadas y grande para la gente gorda. Las personas con un IMC de 25 o más se consideran con sobrepeso, a menos que tengan un cuerpo muy muscular. El IMC no considera la proporción de grasa y músculo. Una persona muscular con un porcentaje bajo de grasa puede clasificarse incorrectamente como obeso utilizando solamente el IMC. Ésta es una deficiencia bien conocida del IMC. Si su IMC es 25 o mayor, pero su índice cintura/altura es menos de 0.5 y su porcentaje de grasa corporal está en el rango de "deportista" o "fitness", usted es probablemente muscular y no gordo
EJEMPLO 2: ¿Quién es el pelotero más valioso?
El beisbol es un deporte que se juega con una bola dura y un bat entre dos equipos de nueve jugadores cada uno. Un partido de beisbol se divide en nueve periodos de juego, cada uno de los cuales se llama entrada o inning. El equipo que anote más carreras a lo largo de las nueve entradas gana el partido. El juego comienza cuando un jugador llamado lanzador o pitcher, lanza la bola hacia el bateador del equipo contrario quien intenta batear (golpear con el bat) la bola hacia el interior del terreno de juego. Los jugadores anotan carreras bateando la bola y corriendo alrededor de una serie de 4 bases, antes de que les elimine algún jugador de campo del equipo contrario. Si un bateador alcanza una base bateando una bola de forma que los jugadores del equipo contrario no consigan atraparla con éxito, el jugador ha conseguido un hit, y el corredor intenta avanzar, sin que le eliminen, el mayor número de bases posible. El hit con el que el bateador consigue alcanzar la segunda base se llama doble; con el que alcanza la tercera, se llama triple. Si un jugador al batear la bola sale volando por encima de la zona de juego y cae fuera de los límites es un cuadrangular o homerun.
Las entradas están divididas en dos mitades, llamadas principio y final de entrada. Durante el principio de una entrada, un equipo batea mientras el otro está en el campo. Cuando el equipo que batea tenga tres jugadores eliminados, los dos equipos intercambian sus papeles y comienza el final de una entrada. Si el resultado permanece empatado al final de nueve entradas, los dos equipos continúan jugando hasta que, al final de una
o más entradas suplementarias, uno de los dos anote más carreras que el otro.
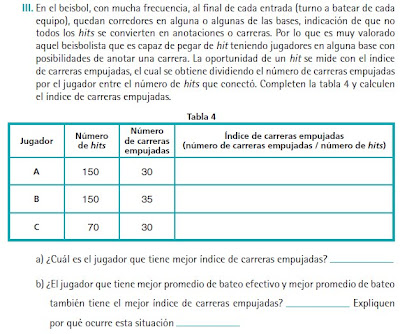
En el caso del beisbol, como en muchos otros, hay situaciones que se miden a partir de varios índices, cada uno de los cuales determina un aspecto diferente de la situación. Por ejemplo, para medir el rendimiento de un jugador de beisbol se necesita conocer la frecuencia, calidad y oportunidad de los hits que “conecta”.
EJEMPLO 3: EL ÍNDICE NACIONAL DE PRECIOS AL CONSUMIDOR
¿Cómo han variado los precios de los alimentos, la ropa, los zapatos y el transporte, durante el año? Con frecuencia esta información la encontramos en la sección financiera de los periódicos y en los noticieros. La presentan generalmente mediante porcentajes, a los que se les llama índices de precios.
Para contestar las preguntas y completar la tabla de los incisos, lean el siguiente artículo publicado el 23 de febrero de 2007 en un periódico de circulación nacional, con los datos del aumento del precio de la tortilla y su repercusión en el Índice Nacional de Precios al Consumidor en la primera quincena de ese mes.
a) De acuerdo con el artículo anterior, ¿qué es lo que mide el Índice Nacional de Precios al Consumidor (INPC)?
b) ¿Cuál fue el valor del repunte del INPC durante la primera quincena de febrero 2007?
c) ¿Y cuál fue el valor del repunte del INPC en ese mismo periodo pero en el año 2006?
d) Completen la siguiente tabla con la información de la variación del precio de la tortilla que aparece en el artículo.
e) Supongan que el precio promedio del kilogramo de tortilla, durante la primera quincena de febrero, fue de $8.50, ¿cuánto costó el precio del kilogramo de tortilla en Torreón en ese mismo periodo?
f) ¿Cuáles son los diferentes índices a que hace referencia el artículo?
g) Anoten una en cada caso si la afirmación es verdadera o falsa:
El INPC puede utilizarse para mostrar la variación en el precio
de algunos productos como el de la tortilla. (V) (F)
El aumento de la inflación durante la primera quincena de febrero
de 2007 fue del doble con respecto a febrero de 2006. (V) (F)
La principal causa del aumento en el valor de la inflación en ese
periodo se atribuye a la variación en el precio de la tortilla. (V) (F)
A continuación se presenta otra noticia relacionada con el INPC que apareció el 20 de septiembre de 2007; léanla y respondan las siguientes preguntas.
a) Según la noticia del periódico, ¿cuántos son los productos que se consideran parte de la canasta básica?
b) De diciembre de 2006 a la fecha en que se publica el artículo, ¿cuál es el repunte de la inflación general?
c) ¿Y cuál es el aumento promedio que ha tenido la gasolina en ese mismo periodo?
d) ¿Por qué creen que organizaciones de consumidores consideran que afectaría el aumento del precio de la gasolina al INPC?
e) Completen la siguiente tabla:
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO
a) ¿Cuál es el estado con mayor porcentaje de deserción escolar?
b) ¿Y cuál es el estado con menor porcentaje de deserción?
c) ¿Cuál es el porcentaje de deserción nacional en secundaria?
d) Con respecto al porcentaje de deserción nacional, ¿cuántos estados están por arriba de él?
e) ¿Cuántos estados están por debajo de él?
a) ¿Cuánto más aumentó la reprobación intracurricular con respecto a la reprobación total en Aguascalientes?
b) ¿En qué entidad o estado la reprobación intracurricular fue mayor?
c) ¿El estado con mayor reprobación total es el mismo que tiene mayor reprobación intracurricular?
d) ¿Qué estado tiene la menor reprobación intracurricular?
a) ¿Cuál grupo de edad tiene el mayor índice de desarrollo social?
¿En qué categoría se encuentra?
b) ¿Cuál es el índice de desarrollo social de la población entre 6 y 14 años?
¿En que categoría se encuentra?
c) ¿Cuál es el menor índice de desarrollo social?
d) ¿Cuál es el grupo de edad a que corresponde ese índice?
e) ¿En qué categoría se encuentran? ¿Por qué crees que este grupo
de edad tiene menor índice de desarrollo social?
EJEMPLO 1: EL ÍNDICE DE MASA CORPORAL
Índice de Masa Corporal (IMC) - El IMC se calcula dividiendo el peso por el cuadrado de la altura. El número da una idea de la proporción del cuerpo. En general, el número es pequeño para las personas delgadas y grande para la gente gorda. Las personas con un IMC de 25 o más se consideran con sobrepeso, a menos que tengan un cuerpo muy muscular. El IMC no considera la proporción de grasa y músculo. Una persona muscular con un porcentaje bajo de grasa puede clasificarse incorrectamente como obeso utilizando solamente el IMC. Ésta es una deficiencia bien conocida del IMC. Si su IMC es 25 o mayor, pero su índice cintura/altura es menos de 0.5 y su porcentaje de grasa corporal está en el rango de "deportista" o "fitness", usted es probablemente muscular y no gordo
EJEMPLO 2: ¿Quién es el pelotero más valioso?
El beisbol es un deporte que se juega con una bola dura y un bat entre dos equipos de nueve jugadores cada uno. Un partido de beisbol se divide en nueve periodos de juego, cada uno de los cuales se llama entrada o inning. El equipo que anote más carreras a lo largo de las nueve entradas gana el partido. El juego comienza cuando un jugador llamado lanzador o pitcher, lanza la bola hacia el bateador del equipo contrario quien intenta batear (golpear con el bat) la bola hacia el interior del terreno de juego. Los jugadores anotan carreras bateando la bola y corriendo alrededor de una serie de 4 bases, antes de que les elimine algún jugador de campo del equipo contrario. Si un bateador alcanza una base bateando una bola de forma que los jugadores del equipo contrario no consigan atraparla con éxito, el jugador ha conseguido un hit, y el corredor intenta avanzar, sin que le eliminen, el mayor número de bases posible. El hit con el que el bateador consigue alcanzar la segunda base se llama doble; con el que alcanza la tercera, se llama triple. Si un jugador al batear la bola sale volando por encima de la zona de juego y cae fuera de los límites es un cuadrangular o homerun.
Las entradas están divididas en dos mitades, llamadas principio y final de entrada. Durante el principio de una entrada, un equipo batea mientras el otro está en el campo. Cuando el equipo que batea tenga tres jugadores eliminados, los dos equipos intercambian sus papeles y comienza el final de una entrada. Si el resultado permanece empatado al final de nueve entradas, los dos equipos continúan jugando hasta que, al final de una
o más entradas suplementarias, uno de los dos anote más carreras que el otro.
En el caso del beisbol, como en muchos otros, hay situaciones que se miden a partir de varios índices, cada uno de los cuales determina un aspecto diferente de la situación. Por ejemplo, para medir el rendimiento de un jugador de beisbol se necesita conocer la frecuencia, calidad y oportunidad de los hits que “conecta”.
EJEMPLO 3: EL ÍNDICE NACIONAL DE PRECIOS AL CONSUMIDOR
¿Cómo han variado los precios de los alimentos, la ropa, los zapatos y el transporte, durante el año? Con frecuencia esta información la encontramos en la sección financiera de los periódicos y en los noticieros. La presentan generalmente mediante porcentajes, a los que se les llama índices de precios.
Para contestar las preguntas y completar la tabla de los incisos, lean el siguiente artículo publicado el 23 de febrero de 2007 en un periódico de circulación nacional, con los datos del aumento del precio de la tortilla y su repercusión en el Índice Nacional de Precios al Consumidor en la primera quincena de ese mes.
a) De acuerdo con el artículo anterior, ¿qué es lo que mide el Índice Nacional de Precios al Consumidor (INPC)?
b) ¿Cuál fue el valor del repunte del INPC durante la primera quincena de febrero 2007?
c) ¿Y cuál fue el valor del repunte del INPC en ese mismo periodo pero en el año 2006?
d) Completen la siguiente tabla con la información de la variación del precio de la tortilla que aparece en el artículo.
e) Supongan que el precio promedio del kilogramo de tortilla, durante la primera quincena de febrero, fue de $8.50, ¿cuánto costó el precio del kilogramo de tortilla en Torreón en ese mismo periodo?
f) ¿Cuáles son los diferentes índices a que hace referencia el artículo?
g) Anoten una en cada caso si la afirmación es verdadera o falsa:
El INPC puede utilizarse para mostrar la variación en el precio
de algunos productos como el de la tortilla. (V) (F)
El aumento de la inflación durante la primera quincena de febrero
de 2007 fue del doble con respecto a febrero de 2006. (V) (F)
La principal causa del aumento en el valor de la inflación en ese
periodo se atribuye a la variación en el precio de la tortilla. (V) (F)
A continuación se presenta otra noticia relacionada con el INPC que apareció el 20 de septiembre de 2007; léanla y respondan las siguientes preguntas.
a) Según la noticia del periódico, ¿cuántos son los productos que se consideran parte de la canasta básica?
b) De diciembre de 2006 a la fecha en que se publica el artículo, ¿cuál es el repunte de la inflación general?
c) ¿Y cuál es el aumento promedio que ha tenido la gasolina en ese mismo periodo?
d) ¿Por qué creen que organizaciones de consumidores consideran que afectaría el aumento del precio de la gasolina al INPC?
e) Completen la siguiente tabla:
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO
a) ¿Cuál es el estado con mayor porcentaje de deserción escolar?
b) ¿Y cuál es el estado con menor porcentaje de deserción?
c) ¿Cuál es el porcentaje de deserción nacional en secundaria?
d) Con respecto al porcentaje de deserción nacional, ¿cuántos estados están por arriba de él?
e) ¿Cuántos estados están por debajo de él?
a) ¿Cuánto más aumentó la reprobación intracurricular con respecto a la reprobación total en Aguascalientes?
b) ¿En qué entidad o estado la reprobación intracurricular fue mayor?
c) ¿El estado con mayor reprobación total es el mismo que tiene mayor reprobación intracurricular?
d) ¿Qué estado tiene la menor reprobación intracurricular?
a) ¿Cuál grupo de edad tiene el mayor índice de desarrollo social?
¿En qué categoría se encuentra?
b) ¿Cuál es el índice de desarrollo social de la población entre 6 y 14 años?
¿En que categoría se encuentra?
c) ¿Cuál es el menor índice de desarrollo social?
d) ¿Cuál es el grupo de edad a que corresponde ese índice?
e) ¿En qué categoría se encuentran? ¿Por qué crees que este grupo
de edad tiene menor índice de desarrollo social?
viernes, 4 de noviembre de 2011
10 Construcción de Figuras Semejantes
Objetivo: En esta secuencia aprenderás cuáles son las condiciones que deben
tener dos figuras para que se diga que son semejantes. Repasarás los criterios de congruencia y semejanza de figuras.
I. Completa tus notas y conclusiones con esta sección:
II. Repasa para tu examen y gánate un punto al resolver los siguientes ejercicios:
tener dos figuras para que se diga que son semejantes. Repasarás los criterios de congruencia y semejanza de figuras.
I. Completa tus notas y conclusiones con esta sección:
II. Repasa para tu examen y gánate un punto al resolver los siguientes ejercicios:
martes, 1 de noviembre de 2011
martes, 25 de octubre de 2011
TEMARIO PARA PRIMER EXAMEN BIMESTRAL
El examen bimestral consistirá en el primer Bimestre del Programa "viejo", por lo que deberán contestar el repaso del bloque 1 viejito (Páginas 38 a la 41).
De todos modos, les dejo aquí los temas:
PRODUCTOS NOTABLES
FACTORIZACIÓN
CRITERIOS DE CONGRUENCIA EN CUADRILÁTEROS
¿CUÁLES SON LAS CARACTERÍSTICAS DE LOS PARALELOGRAMOS?
¿CÓMO SON LOS TRIÁNGULOS INTERIORES QUE SE FORMAN DENTRO DE UN ROMBOIDE CUANDO SE CRUZAN SUS DIAGONALES?
¿QUÉ SIGNIFICA QUE UNA FIGURA SEA SEMEJANTE A OTRA? ¿QUÉ CARACTERÍSTICAS CONSERVAN? ¿QUÉ CARACTERÍSTICAS SON DIFERENTES?
¿CUÁL ES LA PROPIEDAD MÁS IMPORTANTE ENTRE UNA RECTA TANGENTE A UNA CIRCUNFERENCIA Y EL RADIO DE LA MISMA?
¿CUÁL ES LA RELACIÓN QUE EXISTE ENTRE EL ÁNGULO CENTRAL Y EL ÁNGULO INSCRITO DE UNA CIRCUNFERENCIA QUE COMPARTEN EL MISMO ARCO?
RESUELVAN EL EJERCICIO DE LA CABRA, PÁGINA 25
¿CÓMO SE CALCULA LA PENDIENTE DE UNA RECTA?
¿QUÉ ES UNA RAZÓN DE CAMBIO? APLICACIONES CON LA VELOCIDAD.
RESUELVAN EL PROBLEMA DE LOS TELÉFONOS, PÁGINA 31
RECUERDEN LAS POSICIONES RELATIVAS ENTRE DOS CIRCUNFERENCIAS (EN UN ECLIPSE)
RESUELVAN LOS PROBLEMAS DE LA PÁGINA 45.
¿QUÉ ES Y PAR QUÉ SE USA UNA GRÁFICA CIRCULAR (DE PASTEL O DE SECTORES), UNA GRÁFICA DE BARRAS, UNA GRÁFICA POLIGONAL O DE LÍNEA, Y UN PICTOGRAMA.
De todos modos, les dejo aquí los temas:
PRODUCTOS NOTABLES
FACTORIZACIÓN
CRITERIOS DE CONGRUENCIA EN CUADRILÁTEROS
¿CUÁLES SON LAS CARACTERÍSTICAS DE LOS PARALELOGRAMOS?
¿CÓMO SON LOS TRIÁNGULOS INTERIORES QUE SE FORMAN DENTRO DE UN ROMBOIDE CUANDO SE CRUZAN SUS DIAGONALES?
¿QUÉ SIGNIFICA QUE UNA FIGURA SEA SEMEJANTE A OTRA? ¿QUÉ CARACTERÍSTICAS CONSERVAN? ¿QUÉ CARACTERÍSTICAS SON DIFERENTES?
¿CUÁL ES LA PROPIEDAD MÁS IMPORTANTE ENTRE UNA RECTA TANGENTE A UNA CIRCUNFERENCIA Y EL RADIO DE LA MISMA?
¿CUÁL ES LA RELACIÓN QUE EXISTE ENTRE EL ÁNGULO CENTRAL Y EL ÁNGULO INSCRITO DE UNA CIRCUNFERENCIA QUE COMPARTEN EL MISMO ARCO?
RESUELVAN EL EJERCICIO DE LA CABRA, PÁGINA 25
¿CÓMO SE CALCULA LA PENDIENTE DE UNA RECTA?
¿QUÉ ES UNA RAZÓN DE CAMBIO? APLICACIONES CON LA VELOCIDAD.
RESUELVAN EL PROBLEMA DE LOS TELÉFONOS, PÁGINA 31
RECUERDEN LAS POSICIONES RELATIVAS ENTRE DOS CIRCUNFERENCIAS (EN UN ECLIPSE)
RESUELVAN LOS PROBLEMAS DE LA PÁGINA 45.
¿QUÉ ES Y PAR QUÉ SE USA UNA GRÁFICA CIRCULAR (DE PASTEL O DE SECTORES), UNA GRÁFICA DE BARRAS, UNA GRÁFICA POLIGONAL O DE LÍNEA, Y UN PICTOGRAMA.
jueves, 20 de octubre de 2011
09 Probabilidad
Momento 1
Raúl está de vacaciones y desea convivir con sus amigos yendo a nadar el miércoles. Sin embargo, las predicciones del clima hechas el domingo reportan que las probabilidades de lluvia serán de 50% para el lunes, 25% para el martes y 25 % para el miércoles. Sus padres no lo quieren dejar ir, ya que consideran que el miércoles estará lloviendo. A pesar de la negativa de sus padres, Raúl está buscando una estrategia para convencerlos de que no será así. Si estuvieras en el caso de Raúl ¿qué tipo de argumentación podrías construir para obtener el permiso? Comenta tu estrategia.
Momento 2
Uno de los argumentos que le dio su padre para no dejarlo ir fue el hecho de que las probabilidades de lluvia para el lunes, martes y miércoles son 50%, 25% y 25% respectivamente, lo que se resume en una probabilidad del 100% de lluvia para los próximos tres días.
¿Consideras que el resultado del clima para el miércoles se comportará como establece el padre de Raúl? ¿Por qué? Comparte y argumenta tu respuesta.
Si llovió lunes, martes y miércoles ¿Cuál será la probabilidad de que el jueves llueva?
Momento 3
Indicaciones. Si tienes tres urnas organizadas de la siguiente manera:
• ¿Cuál es la probabilidad de que saques una bola blanca de la urna 1?
Si realizas tres extracciones de cada urna:
• Si la composición de la urna 1 cambia y ahora es de 6 bolas blancas y 6 bolas negras
¿Cambia la probabilidad de sacar una bola blanca? Argumenta tu respuesta.
• ¿Cuál es la probabilidad de que saques una bola blanca de la urna 2?
• Si la composición de la urna 2 cambia y ahora es de 4 bolas blancas y 12 bolas negras
¿Cambia la probabilidad de sacar una bola blanca? Fundamenta tu respuesta.
• ¿Cuál es la probabilidad de que saques una bola blanca de la urna 3?
Momento 4
El siguiente diagrama representa una rama del árbol, que alude al experimento de extraer una bola de cada urna, en términos de las probabilidades anteriores. Analiza y discute con tus compañeros, el diagrama. Toma en cuenta que la letra N representa las bolas negras y la letra B representa las bolas blancas.
¿Cuál es la probabilidad de obtener una bola blanca en la tercera urna, si ya has sacado una blanca de la primera y una blanca de la segunda? Utiliza la información anterior.
Momento 6
Indicaciones. Reflexiona en términos de los tipos de fenómenos, los eventos, las probabilidades, las argumentaciones de los momentos 1 y 3, y realiza una comparación entre ambos. Comenta y compara tus resultados.
Raúl está de vacaciones y desea convivir con sus amigos yendo a nadar el miércoles. Sin embargo, las predicciones del clima hechas el domingo reportan que las probabilidades de lluvia serán de 50% para el lunes, 25% para el martes y 25 % para el miércoles. Sus padres no lo quieren dejar ir, ya que consideran que el miércoles estará lloviendo. A pesar de la negativa de sus padres, Raúl está buscando una estrategia para convencerlos de que no será así. Si estuvieras en el caso de Raúl ¿qué tipo de argumentación podrías construir para obtener el permiso? Comenta tu estrategia.
Momento 2
Uno de los argumentos que le dio su padre para no dejarlo ir fue el hecho de que las probabilidades de lluvia para el lunes, martes y miércoles son 50%, 25% y 25% respectivamente, lo que se resume en una probabilidad del 100% de lluvia para los próximos tres días.
¿Consideras que el resultado del clima para el miércoles se comportará como establece el padre de Raúl? ¿Por qué? Comparte y argumenta tu respuesta.
Si llovió lunes, martes y miércoles ¿Cuál será la probabilidad de que el jueves llueva?
Momento 3
Indicaciones. Si tienes tres urnas organizadas de la siguiente manera:
• ¿Cuál es la probabilidad de que saques una bola blanca de la urna 1?
Si realizas tres extracciones de cada urna:
• Si la composición de la urna 1 cambia y ahora es de 6 bolas blancas y 6 bolas negras
¿Cambia la probabilidad de sacar una bola blanca? Argumenta tu respuesta.
• ¿Cuál es la probabilidad de que saques una bola blanca de la urna 2?
• Si la composición de la urna 2 cambia y ahora es de 4 bolas blancas y 12 bolas negras
¿Cambia la probabilidad de sacar una bola blanca? Fundamenta tu respuesta.
• ¿Cuál es la probabilidad de que saques una bola blanca de la urna 3?
Momento 4
El siguiente diagrama representa una rama del árbol, que alude al experimento de extraer una bola de cada urna, en términos de las probabilidades anteriores. Analiza y discute con tus compañeros, el diagrama. Toma en cuenta que la letra N representa las bolas negras y la letra B representa las bolas blancas.
¿Cuál es la probabilidad de obtener una bola blanca en la tercera urna, si ya has sacado una blanca de la primera y una blanca de la segunda? Utiliza la información anterior.
Momento 6
Indicaciones. Reflexiona en términos de los tipos de fenómenos, los eventos, las probabilidades, las argumentaciones de los momentos 1 y 3, y realiza una comparación entre ambos. Comenta y compara tus resultados.
lunes, 17 de octubre de 2011
EL ABC DEL APRENDIZAJE
"Es verdad que ninguna disciplina al momento de recibirla, parece agradable, sino más bien causa de tristeza; sin embargo, después produce fruto de justicia y paz para quienes han sido entrenados por ella"
La Biblia
A punta con atención el tema nuevo.
B log para completar tus notas.
C ontesta Ejercicios, Repaso (Gánate 1 punto) y Tarea Extra.
D udas se resuelve en Asesoría (Jueves SAM, Viernes ANDES)
É xito en el examen quincenal.
¿Cómo impacta en mi calificación?
APUNTA
*Ponga el título y fecha con rojo, tome nota de lo más relevante.
*Su participación hace la diferencia entre una clase aburrida y una interesante.
BLOG
*Si no considera los ejemplos, ejercicios, imágenes y conclusiones del Blog para completar sus notas se calificará su cuaderno sobre 8
*(En Noviembre será sobre 7, en diciembre será sobre 6, etc.)
CONTESTA
*Todos los días deberá llevarse su cuaderno de ejercicios para trabajar en su TAREA 15 minutos diarios en casa.
*Por ningún motivo lo deje en su casillero.
* El REPASO es REQUISITO PARA PODER PRESENTAR EXAMEN (Esto está autorizado por Coordinación de Secundaria)
* La TAREA EXTRA es otra manera de ganar puntos y resolver problemas más difíciles. La Tarea extra es obligatoria para Mate 3 Nivel Intermedio-Andes. Es opcional para Ciencias 2 y Mate 2. Aunque no sé si algún alumno del SAM se atreva a intentarla.
DUDAS
*El estudiante tiene el derecho de una asesoría PREVIA AL EXAMEN.
*Estudiante que reprueba un examen anterior está obligado a asistir a asesoría.
* Todos los estudiantes de Mate 2 (excepto las cuatro alumnas más responsables el grupo) están obligados a ir a asesoría.
* En caso de no poder ir a asesoría, debe presentar un justificante con nombre y firma del padre de familia y el REPASO RESUELTO el día de la asesoría por la mañana. De otro modo, pierde el punto y el derecho a presentar examen.
ÉXITO
* Los exámenes ya no serán semanales, sino quincenales.
* El profesor se compromete a respaldar el trabajo de cualquier alumno que se someta a este proceso.
Les deseo éxito y que Dios bendiga todo su trabajo y esfuerzo.
De antemano, muchas gracias por su esfuerzo.
Prof. Amir Madrid
Comentarios. amirmkt@yahoo.com.mx
La Biblia
A punta con atención el tema nuevo.
B log para completar tus notas.
C ontesta Ejercicios, Repaso (Gánate 1 punto) y Tarea Extra.
D udas se resuelve en Asesoría (Jueves SAM, Viernes ANDES)
É xito en el examen quincenal.
¿Cómo impacta en mi calificación?
APUNTA
*Ponga el título y fecha con rojo, tome nota de lo más relevante.
*Su participación hace la diferencia entre una clase aburrida y una interesante.
BLOG
*Si no considera los ejemplos, ejercicios, imágenes y conclusiones del Blog para completar sus notas se calificará su cuaderno sobre 8
*(En Noviembre será sobre 7, en diciembre será sobre 6, etc.)
CONTESTA
*Todos los días deberá llevarse su cuaderno de ejercicios para trabajar en su TAREA 15 minutos diarios en casa.
*Por ningún motivo lo deje en su casillero.
* El REPASO es REQUISITO PARA PODER PRESENTAR EXAMEN (Esto está autorizado por Coordinación de Secundaria)
* La TAREA EXTRA es otra manera de ganar puntos y resolver problemas más difíciles. La Tarea extra es obligatoria para Mate 3 Nivel Intermedio-Andes. Es opcional para Ciencias 2 y Mate 2. Aunque no sé si algún alumno del SAM se atreva a intentarla.
DUDAS
*El estudiante tiene el derecho de una asesoría PREVIA AL EXAMEN.
*Estudiante que reprueba un examen anterior está obligado a asistir a asesoría.
* Todos los estudiantes de Mate 2 (excepto las cuatro alumnas más responsables el grupo) están obligados a ir a asesoría.
* En caso de no poder ir a asesoría, debe presentar un justificante con nombre y firma del padre de familia y el REPASO RESUELTO el día de la asesoría por la mañana. De otro modo, pierde el punto y el derecho a presentar examen.
ÉXITO
* Los exámenes ya no serán semanales, sino quincenales.
* El profesor se compromete a respaldar el trabajo de cualquier alumno que se someta a este proceso.
Les deseo éxito y que Dios bendiga todo su trabajo y esfuerzo.
De antemano, muchas gracias por su esfuerzo.
Prof. Amir Madrid
Comentarios. amirmkt@yahoo.com.mx
domingo, 16 de octubre de 2011
08 Diseño de experimentos y estudios estadísticos.
Propósito: En esta secuencia aprenderás que, para obtener información confiable en un experimento o estudio estadístico, es conveniente reflexionar sobre los procedimientos y herramientas que se utilizaran para recopilar, organizar y representar los datos que se obtengan en cada etapa
que conforma al experimento o estudio en cuestion.
Los estudios estadísticos nos permiten investigar sobre diversas situaciones o fenómenos.
Por medio de un estudio estadístico adecuado, lo mismo podemos conocer los efectos que provoca una determinada sustancia en los seres vivos, que el comportamiento del mercado ante un determinado producto o servicio así como, conocer las preferencias de un determinado grupo o sector.
Una fase importante del estudio, dado que es el inicio, es determinar cuál es la pregunta o el problema que se quiere estudiar y la manera en que se obtendrán los datos.
a) ¿Cuál de las encuestas anteriores utilizarías para obtener datos con los que puedas analizar los siguientes temas? Anota A o B en cada tema para indicar que es la encuesta A o la encuesta B, según consideres.
Temas
*Nivel de aprovechamiento y desempeño de los estudiantes.
*Intereses e inquietudes de los estudiantes en su escuela.
*Hábitos de estudio de los estudiantes de secundaria.
*Preferencia acerca de las materias que cursan los estudiantes.
Justifica tu respuesta.
b) De acuerdo con lo que anotaste en el inciso anterior, si se pretende estudiar los intereses e inquietudes de los estudiantes, ¿será suficiente con los datos que se obtengan de las dos preguntas de la encuesta que elegiste? ¿Por qué?
c) ¿Qué tipo de respuestas se pueden obtener al realizar la encuesta B? Anota algunos ejemplos de posibles respuestas.
d) Si se quiere recopilar datos para investigar sobre los hábitos de estudio de los estudiantes de secundaria, ¿qué otras preguntas consideras sería necesario incluir en la encuesta?
¿Por qué es importante hacer las preguntas que sugieres?
e) Si el tema que se pretende estudiar comprende intereses e inquietudes de los estudiantes. ¿Cuáles esperas que sean los de tus compañeros?
Recuerden que:
En general, los datos que se obtienen en un estudio o experimento pueden ser de dos tipos,
cualitativos (por ejemplo, el color de cabello, ojos o piel) o cuantitativos (por ejemplo, la edad, el peso y la estatura de una persona).
En ambos casos se pueden organizar en tablas de frecuencia absoluta, relativa o porcentaje.
Cuando el conjunto de datos es cuantitativo y grande se puede organizar
en tablas de datos agrupados en intervalos.
Recuerden que:
Una gráfica de barras se utiliza para presentar y comparar frecuencias con que ocurre una cualidad o atributo.
Una gráfica circular sirve para comparar qué fracción de un todo es cada parte.
Un histograma presenta datos agrupados en intervalos; cuando éstos son iguales, la altura de cada barra indica su frecuencia.
Un polígono de frecuencias también muestra la frecuencia absoluta, relativa o porcentaje de datos agrupados.
Una gráfica de línea presenta las variaciones en el tiempo.
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO
El agua que proviene de los alimentos que comemos y de los líquidos que bebemos constituye casi la totalidad del agua diaria que utiliza nuestro organismo. En general, se recomienda consumir 2 de agua diariamente.
Internacional Life Sciences Institute (ILSI) es una organización científica no lucrativa que promueve el entendimiento y solución de problemas de interés común en las áreas de nutrición, toxicología, alimentos y seguridad ambiental. En 2004, el ILSI de México, A.C.
publicó el documento titulado “Hidratación: líquidos para la vida”, en el que se presentan recomendaciones actuales para el consumo de agua, con especificaciones de acuerdo con la edad y el sexo.
Consideremos lo siguiente
a) ¿Conoces qué cantidad de agua consumes diariamente? ¿Es la cantidad recomendada?
b) ¿Y tus compañeros saben si están consumiendo una cantidad de agua adecuada?
c) ¿Quiénes consumen más agua, los varones o las mujeres del grupo? ¿Cómo podrías recopilar información para conocer qué cantidad de agua estás consumiendo?
Manos a la obra
I. Discutan las siguientes preguntas:
a) ¿Cómo podrían averiguar la cantidad de agua que consumen sus compañeros de clase? Es decir, ¿será suficiente con preguntar cuántos vasos con agua toman al día? ¿Por qué?
b) ¿Qué unidad de capacidad será conveniente utilizar para registrar los datos que obtengan de las respuestas de los compañeros?
c) Si alguien consume un refresco de 375 ml, ¿está consumiendo agua?
d) ¿Comes consomé o sopa aguada diariamente?
e) ¿Cómo medirán la cantidad de agua que se consume en una sopa aguada o consomé?
En el documento "Hidratación: líquidos para la vida" se incluye el contenido de agua de algunos alimentos y bebidas que se consideran son de consumo habitual.
"Ingestión de agua a partir de alimentos y bebidas consumidos frecuentemente"
¿De qué manera podrían utilizar esta información para determinar, aproximadamente, la cantidad de agua que consumen diariamente?
f) Una vez que decidan la forma en que recopilarán los datos, será conveniente organizarlos y clasificarlos, ¿qué tipo de tabla es más conveniente utilizar para mostrar los resultados de cada pregunta que realicen? Y, ¿qué tipo de gráfica es más conveniente utilizar?
g) ¿Cuál es el consumo promedio (media) diario de agua a través de los alimentos entre tus compañeros?
h) ¿Cuál es el consumo diario de agua más frecuente (moda) entre tus compañeros?
i) Una vez que han obtenido los valores del consumo promedio y del consumo diario más frecuente de agua de los alumnos de su grupo, ¿se confirma la suposición que hicieron en cuanto si la cantidad promedio de agua que consumen es la adecuada?
j) Escriban en sus cuadernos sus conclusiones sobre los resultados que obtuvieron en este estudio sobre el consumo diario de agua entre tus compañeros. Deberán incluir las tablas o gráficas que elaboraron para mostrar sus resultados.
Para saber más
Sobre cómo elaborar una encuesta, consulten:
http://www.encuestafacil.com
[Fecha de consulta: 1 de abril de 2008].
Elijan el icono Diseña y paso a paso podrán elaborar una encuesta.
Sobre algunos estudios estadísticos, consulten:
http://matematicas.mty.itesm.mx/uneest/home.htm
[Fecha de consulta: 1 de abril de 2008].
Ruta: Servicios Ratings de Radio en Monterrey (Presentación en Power Point), Contenido del Reporte Tecnológico de Monterrey.
que conforma al experimento o estudio en cuestion.
Los estudios estadísticos nos permiten investigar sobre diversas situaciones o fenómenos.
Por medio de un estudio estadístico adecuado, lo mismo podemos conocer los efectos que provoca una determinada sustancia en los seres vivos, que el comportamiento del mercado ante un determinado producto o servicio así como, conocer las preferencias de un determinado grupo o sector.
Una fase importante del estudio, dado que es el inicio, es determinar cuál es la pregunta o el problema que se quiere estudiar y la manera en que se obtendrán los datos.
a) ¿Cuál de las encuestas anteriores utilizarías para obtener datos con los que puedas analizar los siguientes temas? Anota A o B en cada tema para indicar que es la encuesta A o la encuesta B, según consideres.
Temas
*Nivel de aprovechamiento y desempeño de los estudiantes.
*Intereses e inquietudes de los estudiantes en su escuela.
*Hábitos de estudio de los estudiantes de secundaria.
*Preferencia acerca de las materias que cursan los estudiantes.
Justifica tu respuesta.
b) De acuerdo con lo que anotaste en el inciso anterior, si se pretende estudiar los intereses e inquietudes de los estudiantes, ¿será suficiente con los datos que se obtengan de las dos preguntas de la encuesta que elegiste? ¿Por qué?
c) ¿Qué tipo de respuestas se pueden obtener al realizar la encuesta B? Anota algunos ejemplos de posibles respuestas.
d) Si se quiere recopilar datos para investigar sobre los hábitos de estudio de los estudiantes de secundaria, ¿qué otras preguntas consideras sería necesario incluir en la encuesta?
¿Por qué es importante hacer las preguntas que sugieres?
e) Si el tema que se pretende estudiar comprende intereses e inquietudes de los estudiantes. ¿Cuáles esperas que sean los de tus compañeros?
Recuerden que:
En general, los datos que se obtienen en un estudio o experimento pueden ser de dos tipos,
cualitativos (por ejemplo, el color de cabello, ojos o piel) o cuantitativos (por ejemplo, la edad, el peso y la estatura de una persona).
En ambos casos se pueden organizar en tablas de frecuencia absoluta, relativa o porcentaje.
Cuando el conjunto de datos es cuantitativo y grande se puede organizar
en tablas de datos agrupados en intervalos.
Recuerden que:
Una gráfica de barras se utiliza para presentar y comparar frecuencias con que ocurre una cualidad o atributo.
Una gráfica circular sirve para comparar qué fracción de un todo es cada parte.
Un histograma presenta datos agrupados en intervalos; cuando éstos son iguales, la altura de cada barra indica su frecuencia.
Un polígono de frecuencias también muestra la frecuencia absoluta, relativa o porcentaje de datos agrupados.
Una gráfica de línea presenta las variaciones en el tiempo.
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO
El agua que proviene de los alimentos que comemos y de los líquidos que bebemos constituye casi la totalidad del agua diaria que utiliza nuestro organismo. En general, se recomienda consumir 2 de agua diariamente.
Internacional Life Sciences Institute (ILSI) es una organización científica no lucrativa que promueve el entendimiento y solución de problemas de interés común en las áreas de nutrición, toxicología, alimentos y seguridad ambiental. En 2004, el ILSI de México, A.C.
publicó el documento titulado “Hidratación: líquidos para la vida”, en el que se presentan recomendaciones actuales para el consumo de agua, con especificaciones de acuerdo con la edad y el sexo.
Consideremos lo siguiente
a) ¿Conoces qué cantidad de agua consumes diariamente? ¿Es la cantidad recomendada?
b) ¿Y tus compañeros saben si están consumiendo una cantidad de agua adecuada?
c) ¿Quiénes consumen más agua, los varones o las mujeres del grupo? ¿Cómo podrías recopilar información para conocer qué cantidad de agua estás consumiendo?
Manos a la obra
I. Discutan las siguientes preguntas:
a) ¿Cómo podrían averiguar la cantidad de agua que consumen sus compañeros de clase? Es decir, ¿será suficiente con preguntar cuántos vasos con agua toman al día? ¿Por qué?
b) ¿Qué unidad de capacidad será conveniente utilizar para registrar los datos que obtengan de las respuestas de los compañeros?
c) Si alguien consume un refresco de 375 ml, ¿está consumiendo agua?
d) ¿Comes consomé o sopa aguada diariamente?
e) ¿Cómo medirán la cantidad de agua que se consume en una sopa aguada o consomé?
En el documento "Hidratación: líquidos para la vida" se incluye el contenido de agua de algunos alimentos y bebidas que se consideran son de consumo habitual.
"Ingestión de agua a partir de alimentos y bebidas consumidos frecuentemente"
¿De qué manera podrían utilizar esta información para determinar, aproximadamente, la cantidad de agua que consumen diariamente?
f) Una vez que decidan la forma en que recopilarán los datos, será conveniente organizarlos y clasificarlos, ¿qué tipo de tabla es más conveniente utilizar para mostrar los resultados de cada pregunta que realicen? Y, ¿qué tipo de gráfica es más conveniente utilizar?
g) ¿Cuál es el consumo promedio (media) diario de agua a través de los alimentos entre tus compañeros?
h) ¿Cuál es el consumo diario de agua más frecuente (moda) entre tus compañeros?
i) Una vez que han obtenido los valores del consumo promedio y del consumo diario más frecuente de agua de los alumnos de su grupo, ¿se confirma la suposición que hicieron en cuanto si la cantidad promedio de agua que consumen es la adecuada?
j) Escriban en sus cuadernos sus conclusiones sobre los resultados que obtuvieron en este estudio sobre el consumo diario de agua entre tus compañeros. Deberán incluir las tablas o gráficas que elaboraron para mostrar sus resultados.
Para saber más
Sobre cómo elaborar una encuesta, consulten:
http://www.encuestafacil.com
[Fecha de consulta: 1 de abril de 2008].
Elijan el icono Diseña y paso a paso podrán elaborar una encuesta.
Sobre algunos estudios estadísticos, consulten:
http://matematicas.mty.itesm.mx/uneest/home.htm
[Fecha de consulta: 1 de abril de 2008].
Ruta: Servicios Ratings de Radio en Monterrey (Presentación en Power Point), Contenido del Reporte Tecnológico de Monterrey.
viernes, 14 de octubre de 2011
07 Función proporcional, lineal y cuadrática.
Propósito: Hasta este momento has estudiado gráficas que son líneas rectas; sin embargo, no todos las gráficas son así. En esta secuencia graficarás relaciones funcionales cuyas gráficas ¡no son líneas rectas!
Repasemos las funciones proporcionales (vistas en primaria y 1er grado) y las funciones lineales (vistas en 2° grado):
I. FUNCIONES PROPORCIONALES
1. A Mario le gusta los gansitos, por lo que consume muchos cada día.
a) Realiza la tabla donde relaciones la cantidad de gansitos comprados (x) con la cantidad a pagar (y).
b) ¿Cuál es la expresión algebraica que relaciona dichas cantidades?
c) Traza la gráfica en GEOGEBRA. ¿Cuál es la forma de la gráfica?
2. “En el periodo vacacional, de una caseta de cobro de la carretera Chilpancingo-Acapulco salen 25 autos por minuto”,
a) ¿Cuántos autos saldrán en una hora? Esta misma afirmación se puede representar de la siguiente manera:
y = número de autos
x = tiempo en minutos
y = 25x
Es decir, el número de autos (y) que pasarán por la caseta es igual a 25 por el tiempo en minutos que midamos.
En nuestro problema original tenemos:
y = 25 (60) y = 1 500 En 60 minutos saldrán 1 500 autos
3. Si el tipo de cambio de un dólar estadounidense por pesos mexicanos es de $14.00. La cantidad de dólares que se cambiarán se representa como x, y la cantidad de pesos que se obtienen se representa como y, entonces la expresión algebraica: y = 14x, permite conocer la cantidad de pesos (y) que se obtiene al cambiar cierta cantidad de dólares (x). La constante de proporcionalidad en este caso es: $14.00 por cada dólar.
a) Elabora la tabla de esta situación.
b) ¿Cuál es la expresión algebraica que relaciona dichas cantidades?
c) Traza la gráfica en GEOGEBRA. ¿Cuál es la forma de la gráfica?
Las gráficas de funciones proporcionales directas son líneas rectas inclinadas que pasan por el origen (0,0).
II. FUNCIONES LINEALES.
Una relación es lineal si su gráfica es una línea recta.
1. Un taxi cobra por su servicio $10.00 más $2.00 por cada kilómetro recorrido.
a) Realiza la tabla donde relaciones la distancia recorrida en km (x) con la cantidad a pagar (y).
b) ¿Cuál es la expresión algebraica que relaciona dichas cantidades?
c) Traza la gráfica en GEOGEBRA. ¿Cuál es la forma de la gráfica?
d) Un pasajero sube al taxi y sólo tiene $32.00, ¿cuántos kilómetros puede viajar?
2. Lee la siguiente receta de cocina: Pavo al horno. Para preparar un pavo suave y jugoso envuélvalo en papel aluminio y hornee 15 minutos por cada kilogramo de pavo y sume a esto 90 minutos extras.
a) ¿Cuánto tiempo de horneado requiere un pavo de 5 kg?
b) ¿Cuánto tiempo de horneado requiere un pavo que pesa 8 kg?
c) ¿Cuánto tiempo de horneado requiere un pavo que pesa 6.5 kg?
d) Completa la siguiente tabla
Peso (Kg) 0 1 2 3 4 5 6 7 8 9 10
Tiempo 90
e) Traza la gráfica en GEOGEBRA. ¿Cuál es la forma de la gráfica?
Las gráficas de funciones lineales son líneas rectas inclinadas que no pasan por el origen (0,0).
III. FUNCIONES CUADRÁTICAS.
¿Cómo caen los cuerpos? El movimiento de caída de una canica a lo largo de un plano inclinado resulta ser uniformemente acelerado, es decir, mantiene
una aceleración constante. Ahora, trataremos de describir la posición
de la canica en cualquier momento del tiempo.
Comparen sus respuestas y comenten.
a) ¿Cuáles de las cuatro gráficas representan relaciones lineales?
b) ¿Cuál de las cuatro representa una relación lineal por pedazos?
En el siguiente plano cartesiano localiza los puntos asociados a la tabla 1. Después dibuja la gráfica de la relación como creas que debería de verse (ayúdate de la gráfica que elegiste en el apartado Consideremos lo siguiente). Recuerda que la gráfica debe pasar por los puntos que ya localizaste.
Observa la gráfica y contesta:
a) Aproximadamente, ¿qué distancia lleva recorrida la canica cuando han transcurrido 2.5 segundos?
b) ¿Y cuando han transcurrido 3.5 segundos?
Denotamos con la letra x el tiempo que ha transcurrido desde que se dejó caer la canica y con la letra y la distancia recorrida. De las siguientes expresiones, ¿cuál crees que sirve para calcular y a partir de x ? Márcala.
a) y = 10x
b) y = 11x^2 – x
c) y = 10x^2
d) y = 30x – 20
Comparen sus respuestas y comenten:
a) Cuando la canica alcanzó el punto más alto, ¿cuál creen que era su velocidad?
b) ¿En qué momento la canica va acelerando?, ¿En qué momento va frenando? ¿Cuándo lleva velocidad constante?
IV. Contesta el siguiente REPASO (Cuenta como cualquier otra tarea), prepárate para tu examen y gánate un punto en el proceso. (Gracias por su esfuerzo y dedicación)
REPASA FUNCIONES PROPORCIONALES
¿Habrá ejemplos donde haya varias relaciones de proporcionalidad presentes en un mismo problema?
Sí, esto lo podemos observar en algunos telescopios y microscopios. Los microscopios compuestos tienen una lente inferior en el objetivo que aumenta 15 veces el tamaño de los objetos. Además, tienen una lente superior en el ocular que aumenta 10 veces.
En la siguiente tabla se organiza la información para visualizar cómo se amplifica el tamaño de algunos objetos en un microscopio, de acuerdo con la información relacionada con los diferentes aumentos, completa la tabla.
En esta tabla hay dos relaciones de proporcionalidad. En sus cuadernos escriban la expresión algebraica que permite:
a) Pasar del tamaño real al tamaño obtenido con la primera lente.
b) Pasar del tamaño real del objeto al tamaño final.
c) Pasar del tamaño obtenido con la primera lente al tamaño obtenido con la segunda lente.
Cuando se aplican sucesivamente dos constantes de proporcionalidad, se obtienen dos relaciones de proporcionalidad. Para cada relación se puede encontrar una expresión algebraica. Por ejemplo, en un microscopio con lentes de 20 y 30 veces de aumento, si se llama:
x al tamaño real
y al tamaño obtenido con la primera lente y
w al tamaño final, se pueden obtener:
*La expresión que permite pasar del tamaño real al tamaño obtenido con la primera lente es: y = 20x
*La expresión que permite pasar del tamaño obtenido con la primera lente al tamaño obtenido con la segunda lente es: w = 30y
*La expresión que permite pasar directamente del tamaño real al tamaño final es: w = 600x
La constante de proporcionalidad de la última expresión se obtiene al multiplicar las constantes dadas por los aumentos de las lentes.
¿Qué otros ejemplos puedes encontrar en tu vida cotidiana?
REPASA FUCIONES LINEALES
En una escuela secundaria quieren rentar un autobús para realizar una excursión. Se solicitó a 3 compañías de autobuses un presupuesto, las cuales proporcionaron la siguiente información:
• Compañía A: cobra $1 500.00 más $20.00 por cada kilómetro recorrido.
• Compañía B: cobra $2 000.00 más $15.00 por cada kilómetro recorrido.
• Compañía C: cobra $3 000.00 más $10.00 por cada kilómetro recorrido.
a) Realiza las tablas de valores para las compañías.
b) ¿Cuáles son las expresiones algebraicas que relacionan el cobro con el número de kilómetros recorridos para cada compañía?
c) Traza la gráfica en GEOGEBRA. ¿Cuál es la forma de la gráfica?
d) ¿En cuál es más barato contratar a la compañía B? Entre ___km y ____km.
REPASA FUNCIONES CUADRÁTICAS
En una empresa fabrican cajas de metal. Las cajas se construyen a partir de una lámina rectangular de 3 m de largo por 2 m de ancho, a la que le cortan cuatro cuadrados de las esquinas. Después, se dobla la lámina restante para formar una caja rectangular y, por último, se sueldan las orillas.
Los fabricantes no saben de qué tamaño cortar los cuadrados para que el volumen sea lo más grande posible. Por ello en la figura se ha marcado con la letra x la medida en metros de los lados de los cuadrados que se cortan.
En este problema encontraremos el valor de x para maximizar la superficie de la base de la caja, es decir, para que su área sea lo más grande posible.
Repasemos las funciones proporcionales (vistas en primaria y 1er grado) y las funciones lineales (vistas en 2° grado):
I. FUNCIONES PROPORCIONALES
1. A Mario le gusta los gansitos, por lo que consume muchos cada día.
a) Realiza la tabla donde relaciones la cantidad de gansitos comprados (x) con la cantidad a pagar (y).
b) ¿Cuál es la expresión algebraica que relaciona dichas cantidades?
c) Traza la gráfica en GEOGEBRA. ¿Cuál es la forma de la gráfica?
2. “En el periodo vacacional, de una caseta de cobro de la carretera Chilpancingo-Acapulco salen 25 autos por minuto”,
a) ¿Cuántos autos saldrán en una hora? Esta misma afirmación se puede representar de la siguiente manera:
y = número de autos
x = tiempo en minutos
y = 25x
Es decir, el número de autos (y) que pasarán por la caseta es igual a 25 por el tiempo en minutos que midamos.
En nuestro problema original tenemos:
y = 25 (60) y = 1 500 En 60 minutos saldrán 1 500 autos
3. Si el tipo de cambio de un dólar estadounidense por pesos mexicanos es de $14.00. La cantidad de dólares que se cambiarán se representa como x, y la cantidad de pesos que se obtienen se representa como y, entonces la expresión algebraica: y = 14x, permite conocer la cantidad de pesos (y) que se obtiene al cambiar cierta cantidad de dólares (x). La constante de proporcionalidad en este caso es: $14.00 por cada dólar.
a) Elabora la tabla de esta situación.
b) ¿Cuál es la expresión algebraica que relaciona dichas cantidades?
c) Traza la gráfica en GEOGEBRA. ¿Cuál es la forma de la gráfica?
Las gráficas de funciones proporcionales directas son líneas rectas inclinadas que pasan por el origen (0,0).
II. FUNCIONES LINEALES.
Una relación es lineal si su gráfica es una línea recta.
1. Un taxi cobra por su servicio $10.00 más $2.00 por cada kilómetro recorrido.
a) Realiza la tabla donde relaciones la distancia recorrida en km (x) con la cantidad a pagar (y).
b) ¿Cuál es la expresión algebraica que relaciona dichas cantidades?
c) Traza la gráfica en GEOGEBRA. ¿Cuál es la forma de la gráfica?
d) Un pasajero sube al taxi y sólo tiene $32.00, ¿cuántos kilómetros puede viajar?
2. Lee la siguiente receta de cocina: Pavo al horno. Para preparar un pavo suave y jugoso envuélvalo en papel aluminio y hornee 15 minutos por cada kilogramo de pavo y sume a esto 90 minutos extras.
a) ¿Cuánto tiempo de horneado requiere un pavo de 5 kg?
b) ¿Cuánto tiempo de horneado requiere un pavo que pesa 8 kg?
c) ¿Cuánto tiempo de horneado requiere un pavo que pesa 6.5 kg?
d) Completa la siguiente tabla
Peso (Kg) 0 1 2 3 4 5 6 7 8 9 10
Tiempo 90
e) Traza la gráfica en GEOGEBRA. ¿Cuál es la forma de la gráfica?
Las gráficas de funciones lineales son líneas rectas inclinadas que no pasan por el origen (0,0).
III. FUNCIONES CUADRÁTICAS.
¿Cómo caen los cuerpos? El movimiento de caída de una canica a lo largo de un plano inclinado resulta ser uniformemente acelerado, es decir, mantiene
una aceleración constante. Ahora, trataremos de describir la posición
de la canica en cualquier momento del tiempo.
Comparen sus respuestas y comenten.
a) ¿Cuáles de las cuatro gráficas representan relaciones lineales?
b) ¿Cuál de las cuatro representa una relación lineal por pedazos?
En el siguiente plano cartesiano localiza los puntos asociados a la tabla 1. Después dibuja la gráfica de la relación como creas que debería de verse (ayúdate de la gráfica que elegiste en el apartado Consideremos lo siguiente). Recuerda que la gráfica debe pasar por los puntos que ya localizaste.
Observa la gráfica y contesta:
a) Aproximadamente, ¿qué distancia lleva recorrida la canica cuando han transcurrido 2.5 segundos?
b) ¿Y cuando han transcurrido 3.5 segundos?
Denotamos con la letra x el tiempo que ha transcurrido desde que se dejó caer la canica y con la letra y la distancia recorrida. De las siguientes expresiones, ¿cuál crees que sirve para calcular y a partir de x ? Márcala.
a) y = 10x
b) y = 11x^2 – x
c) y = 10x^2
d) y = 30x – 20
Comparen sus respuestas y comenten:
a) Cuando la canica alcanzó el punto más alto, ¿cuál creen que era su velocidad?
b) ¿En qué momento la canica va acelerando?, ¿En qué momento va frenando? ¿Cuándo lleva velocidad constante?
IV. Contesta el siguiente REPASO (Cuenta como cualquier otra tarea), prepárate para tu examen y gánate un punto en el proceso. (Gracias por su esfuerzo y dedicación)
REPASA FUNCIONES PROPORCIONALES
¿Habrá ejemplos donde haya varias relaciones de proporcionalidad presentes en un mismo problema?
Sí, esto lo podemos observar en algunos telescopios y microscopios. Los microscopios compuestos tienen una lente inferior en el objetivo que aumenta 15 veces el tamaño de los objetos. Además, tienen una lente superior en el ocular que aumenta 10 veces.
En la siguiente tabla se organiza la información para visualizar cómo se amplifica el tamaño de algunos objetos en un microscopio, de acuerdo con la información relacionada con los diferentes aumentos, completa la tabla.
En esta tabla hay dos relaciones de proporcionalidad. En sus cuadernos escriban la expresión algebraica que permite:
a) Pasar del tamaño real al tamaño obtenido con la primera lente.
b) Pasar del tamaño real del objeto al tamaño final.
c) Pasar del tamaño obtenido con la primera lente al tamaño obtenido con la segunda lente.
Cuando se aplican sucesivamente dos constantes de proporcionalidad, se obtienen dos relaciones de proporcionalidad. Para cada relación se puede encontrar una expresión algebraica. Por ejemplo, en un microscopio con lentes de 20 y 30 veces de aumento, si se llama:
x al tamaño real
y al tamaño obtenido con la primera lente y
w al tamaño final, se pueden obtener:
*La expresión que permite pasar del tamaño real al tamaño obtenido con la primera lente es: y = 20x
*La expresión que permite pasar del tamaño obtenido con la primera lente al tamaño obtenido con la segunda lente es: w = 30y
*La expresión que permite pasar directamente del tamaño real al tamaño final es: w = 600x
La constante de proporcionalidad de la última expresión se obtiene al multiplicar las constantes dadas por los aumentos de las lentes.
¿Qué otros ejemplos puedes encontrar en tu vida cotidiana?
REPASA FUCIONES LINEALES
En una escuela secundaria quieren rentar un autobús para realizar una excursión. Se solicitó a 3 compañías de autobuses un presupuesto, las cuales proporcionaron la siguiente información:
• Compañía A: cobra $1 500.00 más $20.00 por cada kilómetro recorrido.
• Compañía B: cobra $2 000.00 más $15.00 por cada kilómetro recorrido.
• Compañía C: cobra $3 000.00 más $10.00 por cada kilómetro recorrido.
a) Realiza las tablas de valores para las compañías.
b) ¿Cuáles son las expresiones algebraicas que relacionan el cobro con el número de kilómetros recorridos para cada compañía?
c) Traza la gráfica en GEOGEBRA. ¿Cuál es la forma de la gráfica?
d) ¿En cuál es más barato contratar a la compañía B? Entre ___km y ____km.
REPASA FUNCIONES CUADRÁTICAS
En una empresa fabrican cajas de metal. Las cajas se construyen a partir de una lámina rectangular de 3 m de largo por 2 m de ancho, a la que le cortan cuatro cuadrados de las esquinas. Después, se dobla la lámina restante para formar una caja rectangular y, por último, se sueldan las orillas.
Los fabricantes no saben de qué tamaño cortar los cuadrados para que el volumen sea lo más grande posible. Por ello en la figura se ha marcado con la letra x la medida en metros de los lados de los cuadrados que se cortan.
En este problema encontraremos el valor de x para maximizar la superficie de la base de la caja, es decir, para que su área sea lo más grande posible.
lunes, 26 de septiembre de 2011
05 Ecuaciones cuadráticas: Operaciones inversas
ECUACIONES NO LINEALES
Esta semana encontrarás una gran variedad de problemas que no se pueden resolver con ecuaciones lineales, sino que requieren un nuevo tipo de ecuaciones.
Propósito: En esta secuencia resolverás problemas mediante el planteamiento y solución de ecuaciones de segundo o tercer grado.
En Matemáticas I y II aprendiste a resolver problemas y ecuaciones lineales con una incógnita y con dos. Algunas de esas ecuaciones tienen sólo una solución, por ejemplo: 2x + 3 = 8.
Otras tienen una infinidad de soluciones, tal como: x + y = 10.
En esta secuencia estudiarás algunos problemas que pueden resolverse con ecuaciones que tienen dos soluciones, una solución o ninguna solución.
EL NÚMERO SECRETO
I. Resuelve el acertijo:
Pensé un número y lo elevé al cuadrado. Al resultado lo multipliqué por 4 y al final obtuve 100. Si no pensé en el 5, ¿de qué número se trata?
II. El producto de dos números enteros consecutivos es 552.
¿Cuáles son esos números?
a) Para resolver este tipo de problemas es necesario, frecuentemente, encontrar la ecuación primero la ecuación correspondiente. Si se representa con la letra x el número menor de los dos, ¿cuál de las siguientes ecuaciones corresponde al problema anterior?
• (x ) (x ) = 552
• (x ) (552) = y
• x (x + 1) = 552
• (x ) (x ) + 1 = 552
• x^2 + 1 = 552
III. Se tiene el siguiente acertijo: a tres veces el cuadrado de un número se le sumó 8. Como resultado se obtuvo 83.
Si el número se representa con la letra x, ¿cuál de las siguientes es la ecuación que corresponde al acertijo? Subráyala.
• (3 + x )^2 + 8 = 83
• 3x^2 + 8 = 83
• (3)(x^2)(8) = 83
La ecuación que corresponde al acertijo tiene dos posibles soluciones.
a) Encuentra las dos soluciones de la ecuación que subrayaste:
_________ y _________
b) Verifica las soluciones realizando con cada una de ellas las operaciones que se indican en el acertijo.
LO QUE APRENDIMOS DE LAS ECUACIONES CUADRÁTICAS
Resuelve los siguientes problemas. Verifica las soluciones que obtengas.
1. El cuadrado de un número más 3 es igual a 84.
El número puede ser ___________ o ___________
2. Pedro pensó un número, lo elevó al cuadrado, al resultado le sumó 5 y obtuvo 1.
a) ¿Por qué crees que Pedro se equivocó al hacer alguna de las dos operaciones?
b) Si Pedro pensó en el –2, ¿cuánto debió obtener de resultado?
c) Si Pedro pensó en el +2, ¿cuánto debió obtener de resultado?
d) ¿Hay algún número que elevado al cuadrado sea igual a –4? ____ ¿Cuál?
3. El largo de un terreno rectangular mide el doble del ancho. El terreno tiene 162 m^2 de área.
a) Encuentra una ecuación que exprese el problema anterior.
Usa la letra x para representar al ancho.
b) ¿Cuánto mide de ancho?
c) ¿Cuánto mide de largo?
CUBOS, CUADRADOS Y ARISTAS
¿Cuánto mide la arista de un cubo cuyo volumen es 216 cm3?
I. Revisa los procedimientos que siguieron algunos alumnos para resolver el problema.
¿Con cuál de los tres procedimientos estás de acuerdo?
El procedimiento 1 es incorrecto. Aunque es cierto que la expresión que modela el problema es x^3 = 216, no puede obtenerse el valor de x dividiendo entre 3. Es un error común que los alumnos confundan la obtención de una raíz con una división, por ello es importante aclarar que
el procedimiento correcto, en este caso, es buscar un número que elevado al cubo sea igual a 216.
El procedimiento 2 es correcto aunque Rosa no logró obtener una solución. Si hubiese probado con más números entre 5 y 8 posiblemente habría descubierto que 63 = 216.
El procedimiento 3 es correcto aunque Lupe tampoco pudo llegar al resultado. Sin embargo, sabe que siguiendo el procedimiento de operaciones inversas la forma de encontrar el valor de x es sacando la raíz cúbica de 216.
Lo que debe destacarse al discutir los procedimientos 2 y 3 es que aunque ni Rosa ni Lupe llegaron al resultado, la forma de plantear la obtención de la solución es correcta.
Comparen sus respuestas. Comenten:
a) ¿Cuál creen que sea la medida que encontró Rosa al continuar con su procedimiento?
b) ¿Cuánto es la raíz cúbica de 216?
II. Contesta lo que se te pide a continuación
a) Relaciona las columnas.
b) Soluciona las ecuaciones que seleccionaste.
c) Verifica tus soluciones sustituyendo los valores en la siguiente tabla. Si lo consideras necesario, usa tu calculadora.
III. Plantea una ecuación para resolver el siguiente acertijo.
Usa x para representar el número buscado.
"Pensé un número. Le sumé 5 y al resultado lo elevé al cubo.
Al final obtuve –27. ¿Cuál es el número que pensé?"
a) Ecuación: _______________________
b) Soluciona la ecuación que planteaste. Verifica tu solución sustituyendo el valor que encontraste.
Comparen sus respuestas y comenten cómo las encontraron.
LO QUE APRENDIMOS DE LAS ECUACIONES CÚBICAS
Resuelve los siguientes problemas.
1. A un número le resto 15, el resultado lo elevo al cubo y obtengo –8. ¿De qué número se trata?
Ecuación: ________________
Solución: ________________
2. El área total de las seis caras de un cubo es 60 cm^2.
a) Si la medida de una arista se representa con x, ¿cuál de las siguientes ecuaciones permite encontrar la medida de la arista? Subráyala.
• x^3 = 60
• x^2 = 60
• 6x^2 = 60
• 6x = 60
b) ¿Cuánto mide de área, una cara del cubo?
c) ¿Cuánto mide la arista del cubo? x =
(Usa la calculadora para encontrar la solución.)
d) ¿Cuánto mide de volumen el cubo?
III. Gánate un punto al resolver los siguientes problemas de ecuaciones cuadráticas por el método del despeje.
Resuelve los siguientes problemas. Usa la calculadora para realizar las operaciones cuando lo consideres necesario.
1. A un hojalatero le encargaron hacer un recipiente en forma de prisma cuadrangular de 3 dm de altura que tenga un volumen de 48 dm3.
Para construir el recipiente usará una lámina de metal de forma cuadrada (figura A), luego cortará cuadrados en las esquinas y, finalmente, doblará los bordes para formar el recipiente.
Contesta las siguientes preguntas para encontrar las medidas de los lados de la lámina
a) ¿Qué forma geométrica tiene la base del prisma?
b) La medida en decímetros del lado de la lámina es y.
Subraya la expresión que representa la medida, en decímetros, de un lado de la base del prisma?
• y
• y – 6
• y – 3
c) ¿Qué expresión corresponde al área de la base del prisma?
d) Subraya la ecuación que hay que resolver para encontrar la medida de un lado de la lámina metálica.
• 4(y – 6)^2 = 48
• 6(y – 6)^2 = 48
• 3(y – 6)^2 = 48
• 3(y – 3)^2 = 48
e) Hay dos números que solucionan la ecuación que corresponde al problema. Encuéntralos.
y1 = ___________, y2 = ___________
f) ¿Cuánto tiene que medir el lado de la lámina metálica?
2. El parque de una colonia está ubicado en un terreno cuadrado.
El estacionamiento ocupa una parte cuadrada del terreno de 50 m por lado y el resto es el jardín con un área de 14 400 m2.
a) Plantea una ecuación que permita encontrar cuánto mide el lado x de todo el terreno.
b) ¿Cuáles son las dos soluciones de la ecuación que encontraste?
__________ y _____________
c) ¿Cuánto mide el lado del terreno del parque?
3. Inventen dos problemas para cada ecuación, resuélvanlas y determinen cuáles soluciones son aceptables para cada problema.
a) x^2/5 = 125
b) 6a^2 = 37.5
c) 3n^2 – n = 102
Sobre ecuaciones cuadráticas, consulten:
http://www.emathematics.net/es/ecsegundogrado.php?a=1&tipo=numero
Ruta: Ecuación de segundo grado > Resolución cuando b=0
Esta semana encontrarás una gran variedad de problemas que no se pueden resolver con ecuaciones lineales, sino que requieren un nuevo tipo de ecuaciones.
Propósito: En esta secuencia resolverás problemas mediante el planteamiento y solución de ecuaciones de segundo o tercer grado.
En Matemáticas I y II aprendiste a resolver problemas y ecuaciones lineales con una incógnita y con dos. Algunas de esas ecuaciones tienen sólo una solución, por ejemplo: 2x + 3 = 8.
Otras tienen una infinidad de soluciones, tal como: x + y = 10.
En esta secuencia estudiarás algunos problemas que pueden resolverse con ecuaciones que tienen dos soluciones, una solución o ninguna solución.
EL NÚMERO SECRETO
I. Resuelve el acertijo:
Pensé un número y lo elevé al cuadrado. Al resultado lo multipliqué por 4 y al final obtuve 100. Si no pensé en el 5, ¿de qué número se trata?
II. El producto de dos números enteros consecutivos es 552.
¿Cuáles son esos números?
a) Para resolver este tipo de problemas es necesario, frecuentemente, encontrar la ecuación primero la ecuación correspondiente. Si se representa con la letra x el número menor de los dos, ¿cuál de las siguientes ecuaciones corresponde al problema anterior?
• (x ) (x ) = 552
• (x ) (552) = y
• x (x + 1) = 552
• (x ) (x ) + 1 = 552
• x^2 + 1 = 552
III. Se tiene el siguiente acertijo: a tres veces el cuadrado de un número se le sumó 8. Como resultado se obtuvo 83.
Si el número se representa con la letra x, ¿cuál de las siguientes es la ecuación que corresponde al acertijo? Subráyala.
• (3 + x )^2 + 8 = 83
• 3x^2 + 8 = 83
• (3)(x^2)(8) = 83
La ecuación que corresponde al acertijo tiene dos posibles soluciones.
a) Encuentra las dos soluciones de la ecuación que subrayaste:
_________ y _________
b) Verifica las soluciones realizando con cada una de ellas las operaciones que se indican en el acertijo.
LO QUE APRENDIMOS DE LAS ECUACIONES CUADRÁTICAS
Resuelve los siguientes problemas. Verifica las soluciones que obtengas.
1. El cuadrado de un número más 3 es igual a 84.
El número puede ser ___________ o ___________
2. Pedro pensó un número, lo elevó al cuadrado, al resultado le sumó 5 y obtuvo 1.
a) ¿Por qué crees que Pedro se equivocó al hacer alguna de las dos operaciones?
b) Si Pedro pensó en el –2, ¿cuánto debió obtener de resultado?
c) Si Pedro pensó en el +2, ¿cuánto debió obtener de resultado?
d) ¿Hay algún número que elevado al cuadrado sea igual a –4? ____ ¿Cuál?
3. El largo de un terreno rectangular mide el doble del ancho. El terreno tiene 162 m^2 de área.
a) Encuentra una ecuación que exprese el problema anterior.
Usa la letra x para representar al ancho.
b) ¿Cuánto mide de ancho?
c) ¿Cuánto mide de largo?
CUBOS, CUADRADOS Y ARISTAS
¿Cuánto mide la arista de un cubo cuyo volumen es 216 cm3?
I. Revisa los procedimientos que siguieron algunos alumnos para resolver el problema.
¿Con cuál de los tres procedimientos estás de acuerdo?
El procedimiento 1 es incorrecto. Aunque es cierto que la expresión que modela el problema es x^3 = 216, no puede obtenerse el valor de x dividiendo entre 3. Es un error común que los alumnos confundan la obtención de una raíz con una división, por ello es importante aclarar que
el procedimiento correcto, en este caso, es buscar un número que elevado al cubo sea igual a 216.
El procedimiento 2 es correcto aunque Rosa no logró obtener una solución. Si hubiese probado con más números entre 5 y 8 posiblemente habría descubierto que 63 = 216.
El procedimiento 3 es correcto aunque Lupe tampoco pudo llegar al resultado. Sin embargo, sabe que siguiendo el procedimiento de operaciones inversas la forma de encontrar el valor de x es sacando la raíz cúbica de 216.
Lo que debe destacarse al discutir los procedimientos 2 y 3 es que aunque ni Rosa ni Lupe llegaron al resultado, la forma de plantear la obtención de la solución es correcta.
Comparen sus respuestas. Comenten:
a) ¿Cuál creen que sea la medida que encontró Rosa al continuar con su procedimiento?
b) ¿Cuánto es la raíz cúbica de 216?
II. Contesta lo que se te pide a continuación
a) Relaciona las columnas.
b) Soluciona las ecuaciones que seleccionaste.
c) Verifica tus soluciones sustituyendo los valores en la siguiente tabla. Si lo consideras necesario, usa tu calculadora.
III. Plantea una ecuación para resolver el siguiente acertijo.
Usa x para representar el número buscado.
"Pensé un número. Le sumé 5 y al resultado lo elevé al cubo.
Al final obtuve –27. ¿Cuál es el número que pensé?"
a) Ecuación: _______________________
b) Soluciona la ecuación que planteaste. Verifica tu solución sustituyendo el valor que encontraste.
Comparen sus respuestas y comenten cómo las encontraron.
LO QUE APRENDIMOS DE LAS ECUACIONES CÚBICAS
Resuelve los siguientes problemas.
1. A un número le resto 15, el resultado lo elevo al cubo y obtengo –8. ¿De qué número se trata?
Ecuación: ________________
Solución: ________________
2. El área total de las seis caras de un cubo es 60 cm^2.
a) Si la medida de una arista se representa con x, ¿cuál de las siguientes ecuaciones permite encontrar la medida de la arista? Subráyala.
• x^3 = 60
• x^2 = 60
• 6x^2 = 60
• 6x = 60
b) ¿Cuánto mide de área, una cara del cubo?
c) ¿Cuánto mide la arista del cubo? x =
(Usa la calculadora para encontrar la solución.)
d) ¿Cuánto mide de volumen el cubo?
III. Gánate un punto al resolver los siguientes problemas de ecuaciones cuadráticas por el método del despeje.
Resuelve los siguientes problemas. Usa la calculadora para realizar las operaciones cuando lo consideres necesario.
1. A un hojalatero le encargaron hacer un recipiente en forma de prisma cuadrangular de 3 dm de altura que tenga un volumen de 48 dm3.
Para construir el recipiente usará una lámina de metal de forma cuadrada (figura A), luego cortará cuadrados en las esquinas y, finalmente, doblará los bordes para formar el recipiente.
Contesta las siguientes preguntas para encontrar las medidas de los lados de la lámina
a) ¿Qué forma geométrica tiene la base del prisma?
b) La medida en decímetros del lado de la lámina es y.
Subraya la expresión que representa la medida, en decímetros, de un lado de la base del prisma?
• y
• y – 6
• y – 3
c) ¿Qué expresión corresponde al área de la base del prisma?
d) Subraya la ecuación que hay que resolver para encontrar la medida de un lado de la lámina metálica.
• 4(y – 6)^2 = 48
• 6(y – 6)^2 = 48
• 3(y – 6)^2 = 48
• 3(y – 3)^2 = 48
e) Hay dos números que solucionan la ecuación que corresponde al problema. Encuéntralos.
y1 = ___________, y2 = ___________
f) ¿Cuánto tiene que medir el lado de la lámina metálica?
2. El parque de una colonia está ubicado en un terreno cuadrado.
El estacionamiento ocupa una parte cuadrada del terreno de 50 m por lado y el resto es el jardín con un área de 14 400 m2.
a) Plantea una ecuación que permita encontrar cuánto mide el lado x de todo el terreno.
b) ¿Cuáles son las dos soluciones de la ecuación que encontraste?
__________ y _____________
c) ¿Cuánto mide el lado del terreno del parque?
3. Inventen dos problemas para cada ecuación, resuélvanlas y determinen cuáles soluciones son aceptables para cada problema.
a) x^2/5 = 125
b) 6a^2 = 37.5
c) 3n^2 – n = 102
Sobre ecuaciones cuadráticas, consulten:
http://www.emathematics.net/es/ecsegundogrado.php?a=1&tipo=numero
Ruta: Ecuación de segundo grado > Resolución cuando b=0
Suscribirse a:
Comentarios (Atom)