Viernes 25 de noviembre
*Resolverán en parejas el REPASO sobre Teorema de Pitágoras (aunque el día del examen deberán engraparlo junto con el examen de manera individual).
Lunes 28 de noviembre
*Contestarán el examen rápido sobre Índices.
*Si les queda tiempo y no han terminado el REPASO de Teorema de Pitágoras, pueden terminarlo en lo que resta de la clase.
*Recuerden pegar y repasar muy bien los ejemplos del Blog y los ejercicios.
Martes 29 de noviembre
*Resolverán el examen de Teorema de Pitágoras. Tienen toda la hora para contestarlo. No se apresuren.
Miércoles 30 de noviembre
* Llevarán los materiales para trabajar en en su proyecto. Yo les daré el previamente las copias con las especificaciones del mismo.
RECUERDEN QUE:
*En todo momento usar la calculadora para sus actividades. Sólo no está permito el prestarse ningún material durante las actividades o exámenes rápidos.
*SÓLO ALUMNOS ANDES: Hay asesorías para matemáticas 3, este viernes 25 de 5:40 en delante, por si alguno tiene alguno duda sobre el tema de Teorema de Pitágoras, yo estaré en el cuarto piso en el salón de 2° A o 2° B.
miércoles, 23 de noviembre de 2011
lunes, 14 de noviembre de 2011
PROYECTO BIMESTRAL 2
Selecciona junto con tu equipo alguna de las siguientes opciones:
Opción 01: Deberán diseñar y amar tres cajas según las siguientes indicaciones:
Las cajas serán elaboradas con cartón o cartulina pintadas de distinto color.
Indicarán la medida de ancho, longitud, altura de la base y volumen para cada una.
Decidirán para qué podrían utilizarse según sus dimensiones, por ejemplo, para lápices en el escritorio, pañuelos desechables, cuadernos, etc.
Al finalizarlas, realizarán una exposición.
Opción 02: Explicarán un método de solución que sirva para resolver ecuaciones cuadráticas.
Para ello, realizarán una tabla que les ayude a resolver cuatro ecuaciones, las cuales se les mostrarán más adelante.
Opción 03: Diseñarán un póster que contenga figuras y objetos semejantes.
Podrán utilizar materiales de su elección, como cartulina, cartoncillo, papel cascarón o ilustración, lápices de colores, plumones y un juego de geometría para realizar sus dibujos o trazos.
Opción 04: Elaborarán un informe en el que describirán el procedimiento para calcular cuánto mide un objeto o estructura de gran altura.
Para ello deberán elegir un edificio o monumento cuya altura no puedan calcular directamente. Puede ser, por ejemplo, el lugar donde viven (casa, edificio), un árbol muy alto que esté en su localidad, etc.
Deberán presentar al profesor, y a todo el grupo, una fotografía o dibujo del objeto o estructura que eligieron medir y dos estrategias para calcular su altura. Dichas estrategias tendrán que justificarse geométricamente.
Opción 05: Realizarán una investigación del Índice Nacional de Precios al Consumidor (INPC) o del Índice de Desarrollo Social en México, los cuales son muy utilizados para medir la economía y el desarrollo del país.
Entregarán al profesor un reporte de su investigación y explicarán sus resultados ante el grupo.
Opción 06: Diseñarán una manera de simular el juego de la ruleta. Para comenzar consideren una ruleta de cinco colores.
Discutan cómo pueden realizar la simulación del juego de la ruleta, sin tenerla físicamente.
Realizarán un total de 200 simulaciones.
Elaborarán una presentación en la que expliquen cómo llevaron a cabo la simulación y cuáles fueron los resultados que obtuvieron.
Opción 01: Deberán diseñar y amar tres cajas según las siguientes indicaciones:
Las cajas serán elaboradas con cartón o cartulina pintadas de distinto color.
Indicarán la medida de ancho, longitud, altura de la base y volumen para cada una.
Decidirán para qué podrían utilizarse según sus dimensiones, por ejemplo, para lápices en el escritorio, pañuelos desechables, cuadernos, etc.
Al finalizarlas, realizarán una exposición.
Opción 02: Explicarán un método de solución que sirva para resolver ecuaciones cuadráticas.
Para ello, realizarán una tabla que les ayude a resolver cuatro ecuaciones, las cuales se les mostrarán más adelante.
Opción 03: Diseñarán un póster que contenga figuras y objetos semejantes.
Podrán utilizar materiales de su elección, como cartulina, cartoncillo, papel cascarón o ilustración, lápices de colores, plumones y un juego de geometría para realizar sus dibujos o trazos.
Opción 04: Elaborarán un informe en el que describirán el procedimiento para calcular cuánto mide un objeto o estructura de gran altura.
Para ello deberán elegir un edificio o monumento cuya altura no puedan calcular directamente. Puede ser, por ejemplo, el lugar donde viven (casa, edificio), un árbol muy alto que esté en su localidad, etc.
Deberán presentar al profesor, y a todo el grupo, una fotografía o dibujo del objeto o estructura que eligieron medir y dos estrategias para calcular su altura. Dichas estrategias tendrán que justificarse geométricamente.
Opción 05: Realizarán una investigación del Índice Nacional de Precios al Consumidor (INPC) o del Índice de Desarrollo Social en México, los cuales son muy utilizados para medir la economía y el desarrollo del país.
Entregarán al profesor un reporte de su investigación y explicarán sus resultados ante el grupo.
Opción 06: Diseñarán una manera de simular el juego de la ruleta. Para comenzar consideren una ruleta de cinco colores.
Discutan cómo pueden realizar la simulación del juego de la ruleta, sin tenerla físicamente.
Realizarán un total de 200 simulaciones.
Elaborarán una presentación en la que expliquen cómo llevaron a cabo la simulación y cuáles fueron los resultados que obtuvieron.
12 Índices
Objetivo: En esta secuencia aprenderás a interpretar y utilizar índices para explicar el comportamiento de diversas situaciones.
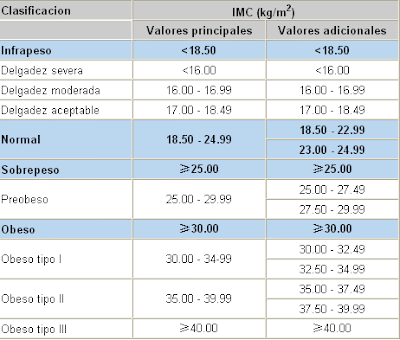
EJEMPLO 1: EL ÍNDICE DE MASA CORPORAL
Índice de Masa Corporal (IMC) - El IMC se calcula dividiendo el peso por el cuadrado de la altura. El número da una idea de la proporción del cuerpo. En general, el número es pequeño para las personas delgadas y grande para la gente gorda. Las personas con un IMC de 25 o más se consideran con sobrepeso, a menos que tengan un cuerpo muy muscular. El IMC no considera la proporción de grasa y músculo. Una persona muscular con un porcentaje bajo de grasa puede clasificarse incorrectamente como obeso utilizando solamente el IMC. Ésta es una deficiencia bien conocida del IMC. Si su IMC es 25 o mayor, pero su índice cintura/altura es menos de 0.5 y su porcentaje de grasa corporal está en el rango de "deportista" o "fitness", usted es probablemente muscular y no gordo
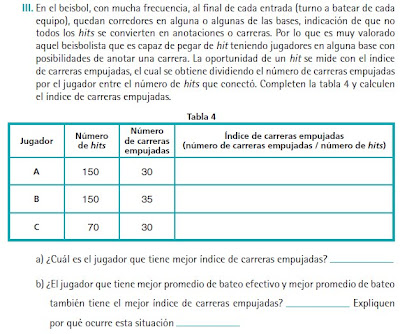
EJEMPLO 2: ¿Quién es el pelotero más valioso?
El beisbol es un deporte que se juega con una bola dura y un bat entre dos equipos de nueve jugadores cada uno. Un partido de beisbol se divide en nueve periodos de juego, cada uno de los cuales se llama entrada o inning. El equipo que anote más carreras a lo largo de las nueve entradas gana el partido. El juego comienza cuando un jugador llamado lanzador o pitcher, lanza la bola hacia el bateador del equipo contrario quien intenta batear (golpear con el bat) la bola hacia el interior del terreno de juego. Los jugadores anotan carreras bateando la bola y corriendo alrededor de una serie de 4 bases, antes de que les elimine algún jugador de campo del equipo contrario. Si un bateador alcanza una base bateando una bola de forma que los jugadores del equipo contrario no consigan atraparla con éxito, el jugador ha conseguido un hit, y el corredor intenta avanzar, sin que le eliminen, el mayor número de bases posible. El hit con el que el bateador consigue alcanzar la segunda base se llama doble; con el que alcanza la tercera, se llama triple. Si un jugador al batear la bola sale volando por encima de la zona de juego y cae fuera de los límites es un cuadrangular o homerun.
Las entradas están divididas en dos mitades, llamadas principio y final de entrada. Durante el principio de una entrada, un equipo batea mientras el otro está en el campo. Cuando el equipo que batea tenga tres jugadores eliminados, los dos equipos intercambian sus papeles y comienza el final de una entrada. Si el resultado permanece empatado al final de nueve entradas, los dos equipos continúan jugando hasta que, al final de una
o más entradas suplementarias, uno de los dos anote más carreras que el otro.
En el caso del beisbol, como en muchos otros, hay situaciones que se miden a partir de varios índices, cada uno de los cuales determina un aspecto diferente de la situación. Por ejemplo, para medir el rendimiento de un jugador de beisbol se necesita conocer la frecuencia, calidad y oportunidad de los hits que “conecta”.
EJEMPLO 3: EL ÍNDICE NACIONAL DE PRECIOS AL CONSUMIDOR
¿Cómo han variado los precios de los alimentos, la ropa, los zapatos y el transporte, durante el año? Con frecuencia esta información la encontramos en la sección financiera de los periódicos y en los noticieros. La presentan generalmente mediante porcentajes, a los que se les llama índices de precios.
Para contestar las preguntas y completar la tabla de los incisos, lean el siguiente artículo publicado el 23 de febrero de 2007 en un periódico de circulación nacional, con los datos del aumento del precio de la tortilla y su repercusión en el Índice Nacional de Precios al Consumidor en la primera quincena de ese mes.
a) De acuerdo con el artículo anterior, ¿qué es lo que mide el Índice Nacional de Precios al Consumidor (INPC)?
b) ¿Cuál fue el valor del repunte del INPC durante la primera quincena de febrero 2007?
c) ¿Y cuál fue el valor del repunte del INPC en ese mismo periodo pero en el año 2006?
d) Completen la siguiente tabla con la información de la variación del precio de la tortilla que aparece en el artículo.
e) Supongan que el precio promedio del kilogramo de tortilla, durante la primera quincena de febrero, fue de $8.50, ¿cuánto costó el precio del kilogramo de tortilla en Torreón en ese mismo periodo?
f) ¿Cuáles son los diferentes índices a que hace referencia el artículo?
g) Anoten una en cada caso si la afirmación es verdadera o falsa:
El INPC puede utilizarse para mostrar la variación en el precio
de algunos productos como el de la tortilla. (V) (F)
El aumento de la inflación durante la primera quincena de febrero
de 2007 fue del doble con respecto a febrero de 2006. (V) (F)
La principal causa del aumento en el valor de la inflación en ese
periodo se atribuye a la variación en el precio de la tortilla. (V) (F)
A continuación se presenta otra noticia relacionada con el INPC que apareció el 20 de septiembre de 2007; léanla y respondan las siguientes preguntas.
a) Según la noticia del periódico, ¿cuántos son los productos que se consideran parte de la canasta básica?
b) De diciembre de 2006 a la fecha en que se publica el artículo, ¿cuál es el repunte de la inflación general?
c) ¿Y cuál es el aumento promedio que ha tenido la gasolina en ese mismo periodo?
d) ¿Por qué creen que organizaciones de consumidores consideran que afectaría el aumento del precio de la gasolina al INPC?
e) Completen la siguiente tabla:
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO
a) ¿Cuál es el estado con mayor porcentaje de deserción escolar?
b) ¿Y cuál es el estado con menor porcentaje de deserción?
c) ¿Cuál es el porcentaje de deserción nacional en secundaria?
d) Con respecto al porcentaje de deserción nacional, ¿cuántos estados están por arriba de él?
e) ¿Cuántos estados están por debajo de él?
a) ¿Cuánto más aumentó la reprobación intracurricular con respecto a la reprobación total en Aguascalientes?
b) ¿En qué entidad o estado la reprobación intracurricular fue mayor?
c) ¿El estado con mayor reprobación total es el mismo que tiene mayor reprobación intracurricular?
d) ¿Qué estado tiene la menor reprobación intracurricular?
a) ¿Cuál grupo de edad tiene el mayor índice de desarrollo social?
¿En qué categoría se encuentra?
b) ¿Cuál es el índice de desarrollo social de la población entre 6 y 14 años?
¿En que categoría se encuentra?
c) ¿Cuál es el menor índice de desarrollo social?
d) ¿Cuál es el grupo de edad a que corresponde ese índice?
e) ¿En qué categoría se encuentran? ¿Por qué crees que este grupo
de edad tiene menor índice de desarrollo social?
EJEMPLO 1: EL ÍNDICE DE MASA CORPORAL
Índice de Masa Corporal (IMC) - El IMC se calcula dividiendo el peso por el cuadrado de la altura. El número da una idea de la proporción del cuerpo. En general, el número es pequeño para las personas delgadas y grande para la gente gorda. Las personas con un IMC de 25 o más se consideran con sobrepeso, a menos que tengan un cuerpo muy muscular. El IMC no considera la proporción de grasa y músculo. Una persona muscular con un porcentaje bajo de grasa puede clasificarse incorrectamente como obeso utilizando solamente el IMC. Ésta es una deficiencia bien conocida del IMC. Si su IMC es 25 o mayor, pero su índice cintura/altura es menos de 0.5 y su porcentaje de grasa corporal está en el rango de "deportista" o "fitness", usted es probablemente muscular y no gordo
EJEMPLO 2: ¿Quién es el pelotero más valioso?
El beisbol es un deporte que se juega con una bola dura y un bat entre dos equipos de nueve jugadores cada uno. Un partido de beisbol se divide en nueve periodos de juego, cada uno de los cuales se llama entrada o inning. El equipo que anote más carreras a lo largo de las nueve entradas gana el partido. El juego comienza cuando un jugador llamado lanzador o pitcher, lanza la bola hacia el bateador del equipo contrario quien intenta batear (golpear con el bat) la bola hacia el interior del terreno de juego. Los jugadores anotan carreras bateando la bola y corriendo alrededor de una serie de 4 bases, antes de que les elimine algún jugador de campo del equipo contrario. Si un bateador alcanza una base bateando una bola de forma que los jugadores del equipo contrario no consigan atraparla con éxito, el jugador ha conseguido un hit, y el corredor intenta avanzar, sin que le eliminen, el mayor número de bases posible. El hit con el que el bateador consigue alcanzar la segunda base se llama doble; con el que alcanza la tercera, se llama triple. Si un jugador al batear la bola sale volando por encima de la zona de juego y cae fuera de los límites es un cuadrangular o homerun.
Las entradas están divididas en dos mitades, llamadas principio y final de entrada. Durante el principio de una entrada, un equipo batea mientras el otro está en el campo. Cuando el equipo que batea tenga tres jugadores eliminados, los dos equipos intercambian sus papeles y comienza el final de una entrada. Si el resultado permanece empatado al final de nueve entradas, los dos equipos continúan jugando hasta que, al final de una
o más entradas suplementarias, uno de los dos anote más carreras que el otro.
En el caso del beisbol, como en muchos otros, hay situaciones que se miden a partir de varios índices, cada uno de los cuales determina un aspecto diferente de la situación. Por ejemplo, para medir el rendimiento de un jugador de beisbol se necesita conocer la frecuencia, calidad y oportunidad de los hits que “conecta”.
EJEMPLO 3: EL ÍNDICE NACIONAL DE PRECIOS AL CONSUMIDOR
¿Cómo han variado los precios de los alimentos, la ropa, los zapatos y el transporte, durante el año? Con frecuencia esta información la encontramos en la sección financiera de los periódicos y en los noticieros. La presentan generalmente mediante porcentajes, a los que se les llama índices de precios.
Para contestar las preguntas y completar la tabla de los incisos, lean el siguiente artículo publicado el 23 de febrero de 2007 en un periódico de circulación nacional, con los datos del aumento del precio de la tortilla y su repercusión en el Índice Nacional de Precios al Consumidor en la primera quincena de ese mes.
a) De acuerdo con el artículo anterior, ¿qué es lo que mide el Índice Nacional de Precios al Consumidor (INPC)?
b) ¿Cuál fue el valor del repunte del INPC durante la primera quincena de febrero 2007?
c) ¿Y cuál fue el valor del repunte del INPC en ese mismo periodo pero en el año 2006?
d) Completen la siguiente tabla con la información de la variación del precio de la tortilla que aparece en el artículo.
e) Supongan que el precio promedio del kilogramo de tortilla, durante la primera quincena de febrero, fue de $8.50, ¿cuánto costó el precio del kilogramo de tortilla en Torreón en ese mismo periodo?
f) ¿Cuáles son los diferentes índices a que hace referencia el artículo?
g) Anoten una en cada caso si la afirmación es verdadera o falsa:
El INPC puede utilizarse para mostrar la variación en el precio
de algunos productos como el de la tortilla. (V) (F)
El aumento de la inflación durante la primera quincena de febrero
de 2007 fue del doble con respecto a febrero de 2006. (V) (F)
La principal causa del aumento en el valor de la inflación en ese
periodo se atribuye a la variación en el precio de la tortilla. (V) (F)
A continuación se presenta otra noticia relacionada con el INPC que apareció el 20 de septiembre de 2007; léanla y respondan las siguientes preguntas.
a) Según la noticia del periódico, ¿cuántos son los productos que se consideran parte de la canasta básica?
b) De diciembre de 2006 a la fecha en que se publica el artículo, ¿cuál es el repunte de la inflación general?
c) ¿Y cuál es el aumento promedio que ha tenido la gasolina en ese mismo periodo?
d) ¿Por qué creen que organizaciones de consumidores consideran que afectaría el aumento del precio de la gasolina al INPC?
e) Completen la siguiente tabla:
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO
a) ¿Cuál es el estado con mayor porcentaje de deserción escolar?
b) ¿Y cuál es el estado con menor porcentaje de deserción?
c) ¿Cuál es el porcentaje de deserción nacional en secundaria?
d) Con respecto al porcentaje de deserción nacional, ¿cuántos estados están por arriba de él?
e) ¿Cuántos estados están por debajo de él?
a) ¿Cuánto más aumentó la reprobación intracurricular con respecto a la reprobación total en Aguascalientes?
b) ¿En qué entidad o estado la reprobación intracurricular fue mayor?
c) ¿El estado con mayor reprobación total es el mismo que tiene mayor reprobación intracurricular?
d) ¿Qué estado tiene la menor reprobación intracurricular?
a) ¿Cuál grupo de edad tiene el mayor índice de desarrollo social?
¿En qué categoría se encuentra?
b) ¿Cuál es el índice de desarrollo social de la población entre 6 y 14 años?
¿En que categoría se encuentra?
c) ¿Cuál es el menor índice de desarrollo social?
d) ¿Cuál es el grupo de edad a que corresponde ese índice?
e) ¿En qué categoría se encuentran? ¿Por qué crees que este grupo
de edad tiene menor índice de desarrollo social?
viernes, 4 de noviembre de 2011
10 Construcción de Figuras Semejantes
Objetivo: En esta secuencia aprenderás cuáles son las condiciones que deben
tener dos figuras para que se diga que son semejantes. Repasarás los criterios de congruencia y semejanza de figuras.
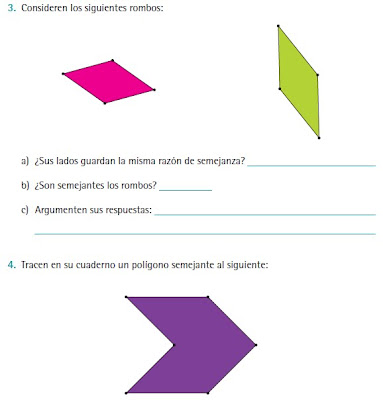
I. Completa tus notas y conclusiones con esta sección:
II. Repasa para tu examen y gánate un punto al resolver los siguientes ejercicios:
tener dos figuras para que se diga que son semejantes. Repasarás los criterios de congruencia y semejanza de figuras.
I. Completa tus notas y conclusiones con esta sección:
II. Repasa para tu examen y gánate un punto al resolver los siguientes ejercicios:
martes, 1 de noviembre de 2011
Suscribirse a:
Comentarios (Atom)