Aprendizaje esperado: Resolución de problemas que implican el uso de ecuaciones cuadráticas. Aplicación de la fórmula general para resolver
dichas ecuaciones.
En las secuencias pasadas resolviste ecuaciones cuadráticas usando tus propios procedimientos, operaciones inversas o la factorización.
Hace varios siglos los matemáticos dedujeron una fórmula para resolver cualquier ecuación cuadrática.
Esta fórmula puede ser muy útil para resolver aquellas ecuaciones en las que resulta difícil utilizar alguno de los procedimientos anteriores.
Sesión 01: ¿Cuál es la fórmula General?
Resuelve el siguiente acertijo:
Luz pensó un número, lo elevó al cuadrado y multiplicó el resultado por 10.
A lo obtenido le sumó tres veces el número que pensó y, al final, para su sorpresa, obtuvo 1. Se sabe que Luz realizó correctamente todas las operaciones.
Hay dos números que pudo haber pensado Luz: ____ o bien ____
Comparen sus soluciones y comenten:
a) ¿Pudieron encontrar los posibles números que pensó Luz?
b) ¿Qué procedimientos usaron para encontrarlos?
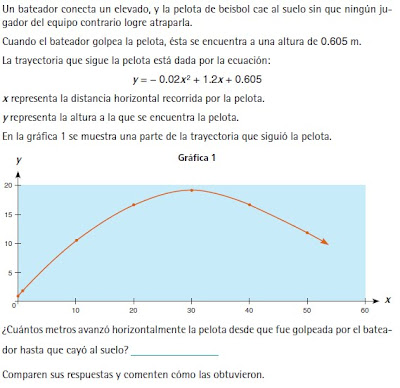
Sesión 02: El beisbolista
Sesión 03: ¿Cuántas soluciones tiene una ecuación?
Mientras que las ecuaciones de primer grado con una incógnita tienen a lo más una solución, las ecuaciones de segundo grado con una incógnita pueden tener dos, una o ninguna solución.
En las sesiones anteriores trabajaste con ecuaciones donde casi todas tenían dos soluciones, ahora trabajarás con ecuaciones que tienen dos, una o ninguna solución. Cuando se usa la fórmula general para resolver una ecuación cuadrática, se puede saber fácilmente cuántas soluciones tiene.
¡Sólo hay que analizar el valor del discriminante: b^2 – 4ac!
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO










Muy buenos ejercicios (Y)
ResponderEliminarLA NETA NO ENTENDI NADAAAAAAAAAAA
ResponderEliminarsolo es cuestión de análisis profundo, le entendí.
ResponderEliminarreprobare :(
ResponderEliminarWata fac
ResponderEliminarWata fac
ResponderEliminarxd
ResponderEliminarLa neta esto es cosa del diablo
ResponderEliminar