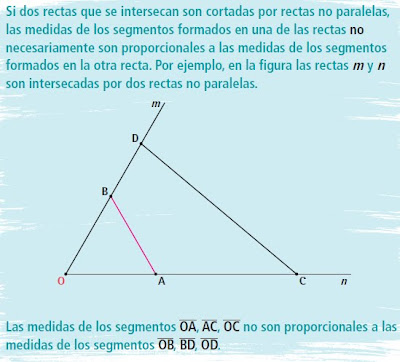
Aprendizaje esperado: En esta secuencia determinarás el teorema de Tales y conocerás cómo dividir un segmento en una razón dada.
Tales de Mileto
Tales es considerado uno de los siete sabios de la antigüedad, junto con Bías de Priene, Quilón de Esparta, Cleóbulo de Lindos, Periandro de Corinto, Pitaco de Mitilene y Solón de Atenas. Tales fue comerciante, filósofo, astrónomo y matemático. A él se atribuye haber enunciado
y probado el resultado matemático llamado Teorema de Tales, que estudiarás en esta secuencia.
a) ¿Estás de acuerdo que con las medidas anotadas se pueden obtener las que faltan? ¿Por qué?
b) Anota en el dibujo de Marta las medidas faltantes.
c) Describe el procedimiento que utilizaste para determinar la medida del segmento A5B5.
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO
Sobre el teorema de Tales y sus aplicaciones, consulta:
http://descartes.cnice.mec.es/materiales_didacticos/Semejanza_aplicaciones/
teorema_de_thales.htm
Sobre Tales, consulta:
http://www.filosofia.org/cur/pre/tales.htm
lunes, 6 de febrero de 2012
viernes, 3 de febrero de 2012
Semejanza de triángulos
Aprendizaje esperado: En esta secuencia aprenderás los criterios de semejanza de triángulos y aplicarás la semejanza de triángulos para calcular distancias inaccesibles.
I. Estudia los siguientes conceptos y ejemplos. Completa los recuadros de acuerdo a lo que se te pide.
En la secuencia 10 aprendiste que para que dos polígonos sean semejantes deben reunir dos condiciones. Anótalas:
1.- _________________________________________________________________
2.- _________________________________________________________________
Discutan y marquen con una "x" en cuáles de los siguientes casos se obtienen necesariamente dos triángulos que son semejantes
Anoten a los que crean que son criterios para establecer que dos triángulos son siempre semejantes. Recuerden que para ser un criterio la o las condiciones deben garantizar que los triángulos siempre son semejantes.
En el recuadro se enunció el tercer criterio de semejanza de triángulos que, junto con los dos que estudiaron en la sesión 2, son los tres criterios de semejanza de triángulos. Hagan un resumen en su cuaderno de los tres criterios e ilústrenlo con triángulos semejantes que cumplan las condiciones dadas en cada uno.
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO
II. Imprime y desarrolla el siguiente REPASO a más tardar el viernes 11 de noviembre.
I. Estudia los siguientes conceptos y ejemplos. Completa los recuadros de acuerdo a lo que se te pide.
En la secuencia 10 aprendiste que para que dos polígonos sean semejantes deben reunir dos condiciones. Anótalas:
1.- _________________________________________________________________
2.- _________________________________________________________________
Discutan y marquen con una "x" en cuáles de los siguientes casos se obtienen necesariamente dos triángulos que son semejantes
Anoten a los que crean que son criterios para establecer que dos triángulos son siempre semejantes. Recuerden que para ser un criterio la o las condiciones deben garantizar que los triángulos siempre son semejantes.
En el recuadro se enunció el tercer criterio de semejanza de triángulos que, junto con los dos que estudiaron en la sesión 2, son los tres criterios de semejanza de triángulos. Hagan un resumen en su cuaderno de los tres criterios e ilústrenlo con triángulos semejantes que cumplan las condiciones dadas en cada uno.
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO
II. Imprime y desarrolla el siguiente REPASO a más tardar el viernes 11 de noviembre.
miércoles, 1 de febrero de 2012
Ecuaciones Cuadráticas (Fórmula General)
Aprendizaje esperado: Resolución de problemas que implican el uso de ecuaciones cuadráticas. Aplicación de la fórmula general para resolver
dichas ecuaciones.
En las secuencias pasadas resolviste ecuaciones cuadráticas usando tus propios procedimientos, operaciones inversas o la factorización.
Hace varios siglos los matemáticos dedujeron una fórmula para resolver cualquier ecuación cuadrática.
Esta fórmula puede ser muy útil para resolver aquellas ecuaciones en las que resulta difícil utilizar alguno de los procedimientos anteriores.
Sesión 01: ¿Cuál es la fórmula General?
Resuelve el siguiente acertijo:
Luz pensó un número, lo elevó al cuadrado y multiplicó el resultado por 10.
A lo obtenido le sumó tres veces el número que pensó y, al final, para su sorpresa, obtuvo 1. Se sabe que Luz realizó correctamente todas las operaciones.
Hay dos números que pudo haber pensado Luz: ____ o bien ____
Comparen sus soluciones y comenten:
a) ¿Pudieron encontrar los posibles números que pensó Luz?
b) ¿Qué procedimientos usaron para encontrarlos?
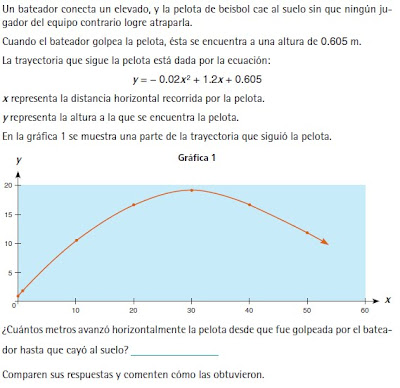
Sesión 02: El beisbolista
Sesión 03: ¿Cuántas soluciones tiene una ecuación?
Mientras que las ecuaciones de primer grado con una incógnita tienen a lo más una solución, las ecuaciones de segundo grado con una incógnita pueden tener dos, una o ninguna solución.
En las sesiones anteriores trabajaste con ecuaciones donde casi todas tenían dos soluciones, ahora trabajarás con ecuaciones que tienen dos, una o ninguna solución. Cuando se usa la fórmula general para resolver una ecuación cuadrática, se puede saber fácilmente cuántas soluciones tiene.
¡Sólo hay que analizar el valor del discriminante: b^2 – 4ac!
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO
dichas ecuaciones.
En las secuencias pasadas resolviste ecuaciones cuadráticas usando tus propios procedimientos, operaciones inversas o la factorización.
Hace varios siglos los matemáticos dedujeron una fórmula para resolver cualquier ecuación cuadrática.
Esta fórmula puede ser muy útil para resolver aquellas ecuaciones en las que resulta difícil utilizar alguno de los procedimientos anteriores.
Sesión 01: ¿Cuál es la fórmula General?
Resuelve el siguiente acertijo:
Luz pensó un número, lo elevó al cuadrado y multiplicó el resultado por 10.
A lo obtenido le sumó tres veces el número que pensó y, al final, para su sorpresa, obtuvo 1. Se sabe que Luz realizó correctamente todas las operaciones.
Hay dos números que pudo haber pensado Luz: ____ o bien ____
Comparen sus soluciones y comenten:
a) ¿Pudieron encontrar los posibles números que pensó Luz?
b) ¿Qué procedimientos usaron para encontrarlos?
Sesión 02: El beisbolista
Sesión 03: ¿Cuántas soluciones tiene una ecuación?
Mientras que las ecuaciones de primer grado con una incógnita tienen a lo más una solución, las ecuaciones de segundo grado con una incógnita pueden tener dos, una o ninguna solución.
En las sesiones anteriores trabajaste con ecuaciones donde casi todas tenían dos soluciones, ahora trabajarás con ecuaciones que tienen dos, una o ninguna solución. Cuando se usa la fórmula general para resolver una ecuación cuadrática, se puede saber fácilmente cuántas soluciones tiene.
¡Sólo hay que analizar el valor del discriminante: b^2 – 4ac!
REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO REPASO
Suscribirse a:
Comentarios (Atom)